题目内容
16.若圆C经过坐标原点和点(4,0),且与直线y=1相切,则圆C的方程是( )| A. | ${(x-2)^2}+{(y+\frac{3}{2})^2}=\frac{25}{4}$ | B. | ${(x-2)^2}+{(y-\frac{3}{2})^2}=\frac{25}{4}$ | ||
| C. | ${(x+2)^2}+{(y-\frac{3}{2})^2}=\frac{25}{4}$ | D. | ${(x+2)^2}+{(y+\frac{3}{2})^2}=\frac{25}{4}$ |
分析 设出圆的圆心坐标与半径,利用已知条件列出方程组,求出圆的圆心坐标与半径,即可得到圆的方程.
解答 解:设圆的圆心坐标(a,b),半径为r,
因为圆C经过坐标原点和点(4,0),且与直线y=1相切,
所以$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}={r}^{2}}\\{(a-4)^{2}+{b}^{2}={r}^{2}}\\{|b-1|=r}\end{array}\right.$,
解得a=2,b=-$\frac{3}{2}$,r=$\frac{5}{2}$,
所求圆的方程为:${(x-2)^2}+{(y+\frac{3}{2})^2}=\frac{25}{4}$.
故选A.
点评 本题考查圆的标准方程的求法,列出方程组是解题的关键,考查计算能力.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
6.若对任意x∈R,都有f(x)<f(x+1),那么f(x)在R上 ( )
| A. | 一定单调递增 | B. | 一定没有单调减区间 | ||
| C. | 可能没有单调增区间 | D. | 一定没有单调增区间 |
4.盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为( )
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
6.已知i是虚数单位,则复数$\frac{2i}{1+i}$的虚部为( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
 如图,已知AB⊥平面BCD,BC⊥CD.求证:
如图,已知AB⊥平面BCD,BC⊥CD.求证: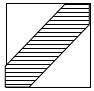 如图,在边长为25cm的正方形中挖去边长为18cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少$\frac{301}{625}$.
如图,在边长为25cm的正方形中挖去边长为18cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少$\frac{301}{625}$.