题目内容
13.已知f(α)=$\frac{cos(2π-α)•sin(\frac{π}{2}+α)}{cos(-α-π)}$.(1)化简f(α);
(2)若f(α)=$\frac{4}{5}$,求cos(π+α)的值.
分析 (1)由已知利用诱导公式化简即可得解.
(2)利用诱导公式化简即可得解.
解答 解:(1)∵f(α)=$\frac{cos(2π-α)•sin(\frac{π}{2}+α)}{cos(-α-π)}$=$\frac{cosα•cosα}{(-cosα)}$=-cosα;
(2)∵f(α)=-cosα=$\frac{4}{5}$,
∴cos(π+α)=-cosα=$\frac{4}{5}$.
点评 本题主要考查了诱导公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
3.设a,b,c为互不相等的正数,则下列不等式不一定成立的是( )
| A. | |a-b|≤|a|+|b| | B. | |a-b|≤|a-c|+|b-c| | C. | $\frac{b}{a}$<$\frac{b+c}{a+c}$ | D. | a2+$\frac{1}{{a}^{2}}$≥a+$\frac{1}{a}$ |
4.盒中有3张分别标有1,2,3的卡片.从盒中随机抽取一张记下号码后放回,再随机抽取一张记下号码,则两次抽取的卡片号码中至少有一个为偶数的概率为( )
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
3.在2015年春节期间,某商场对销售的某商品一天的投放量x及其销量y进行调查,发现投放量x和销售量y之间的一组数据如表所示:
通过分析,发现销售量y对投放量x具有线性相关关系.
(Ⅰ)求销售量y对投放量x的回归直线方程;
(Ⅱ)欲使销售量为8,则投放量应定为多少.(保留小数点后一位数)
| 投放量x | 6 | 8 | 10 | 12 |
| 销售量y | 2 | 3 | 5 | 6 |
(Ⅰ)求销售量y对投放量x的回归直线方程;
(Ⅱ)欲使销售量为8,则投放量应定为多少.(保留小数点后一位数)
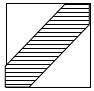 如图,在边长为25cm的正方形中挖去边长为18cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少$\frac{301}{625}$.
如图,在边长为25cm的正方形中挖去边长为18cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少$\frac{301}{625}$.