题目内容
11.已知空间向量$\overrightarrow a=(x,4,3)$,$\overrightarrow b=(3,2,z)$,若$\overrightarrow{a}$∥$\overrightarrow{b}$,则xz=9.分析 根据空间向量的共线定理,列出方程组求出x、z的值,再计算xz的值.
解答 解:空间向量$\overrightarrow a=(x,4,3)$,$\overrightarrow b=(3,2,z)$,
当$\overrightarrow{a}$∥$\overrightarrow{b}$时,$\overrightarrow{a}$=λ$\overrightarrow{b}$,
∴$\left\{\begin{array}{l}{x=3λ}\\{4=2λ}\\{3=λz}\end{array}\right.$,
解得λ=2,x=6,z=$\frac{3}{2}$;
∴xz=6×$\frac{3}{2}$=9.
故答案为:9.
点评 本题考查了空间向量的共线定理与应用问题,是基础题目.

练习册系列答案
相关题目
6.已知i是虚数单位,则复数$\frac{2i}{1+i}$的虚部为( )
| A. | 1 | B. | i | C. | -1 | D. | -i |
3.在2015年春节期间,某商场对销售的某商品一天的投放量x及其销量y进行调查,发现投放量x和销售量y之间的一组数据如表所示:
通过分析,发现销售量y对投放量x具有线性相关关系.
(Ⅰ)求销售量y对投放量x的回归直线方程;
(Ⅱ)欲使销售量为8,则投放量应定为多少.(保留小数点后一位数)
| 投放量x | 6 | 8 | 10 | 12 |
| 销售量y | 2 | 3 | 5 | 6 |
(Ⅰ)求销售量y对投放量x的回归直线方程;
(Ⅱ)欲使销售量为8,则投放量应定为多少.(保留小数点后一位数)
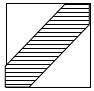 如图,在边长为25cm的正方形中挖去边长为18cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少$\frac{301}{625}$.
如图,在边长为25cm的正方形中挖去边长为18cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少$\frac{301}{625}$. 如图所示,图中曲线方程为y=x2-1,则围成封闭图形(阴影部分)的面积是2.
如图所示,图中曲线方程为y=x2-1,则围成封闭图形(阴影部分)的面积是2. 如图,正四棱锥P-ABCD中底面边长为2$\sqrt{2}$,侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$.
如图,正四棱锥P-ABCD中底面边长为2$\sqrt{2}$,侧棱PA与底面ABCD所成角的正切值为$\frac{{\sqrt{6}}}{2}$.