题目内容

11．若f（x）和g（x）都是定义在R上的函数，则“f（x）与g（x）同是奇函数或同是偶函数”是“f（x）•g（x）是偶函数”的（　　）
A．充分非必要条件B．必要非充分条件
C．充要条件D．既非充分又非必要条件

分析 利用偶函数的判定方法、简易逻辑的判定方法即可得出．

解答 解：由“f（x）与g（x）同是奇函数”可得“f（x）•g（x）是偶函数”；
反之不成立，例如可能f（x）与g（x）同是偶函数．
因此“f（x）与g（x）同是奇函数”是“f（x）•g（x）是偶函数”的充分不必要条件．
故选：A．

点评 本题考查了偶函数的判定方法、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
1．已知奇函数f（x）=$\frac{a•{2}^{x}-1}{{2}^{x}+1}$的定义域为[-a-2，b]
（1）求实数a，b的值；
（2）判断函数f（x）的单调性，并用定义给出证明；
（3）若实数m满足f（m-1）＜f（1-2m），求m的取值范围．
2．已知函数f（x）=$\left\{\begin{array}{l}{2-|x|}，{x≤2}\\{（x-2）^{2}}，{x＞2}\end{array}\right.$，函数g（x）=b-f（2-x），其中b∈R．若函数y=f（x）-g（x）恰有2个零点，则b的取值范围是2＜b，b=$\frac{7}{4}$．
19．下列函数中是奇函数的有几个（　　）
①$y=\frac{{{a^x}+1}}{{{a^x}-1}}$；
②$y=\frac{{lg（{1-{x^2}}）}}{{|{x+3}|-3}}$；
③y=ln|x-1|；
④$y={log_a}\frac{1+x}{1-x}$．
A．1B．2C．3D．4
6．若对任意x∈R，都有f（x）＜f（x+1），那么f（x）在R上 （　　）
A．一定单调递增B．一定没有单调减区间
C．可能没有单调增区间D．一定没有单调增区间
16．已知函数f（x）=lnx．
（1）求f（x）在点（1，f（1））处的切线；
（2）若?x∈[1，+∞），f（x）≤m（${x-\frac{1}{x}}$）恒成立，求实数m的取值范围；
（3）求证：ln（2n+1）＜$\sum_{k=1}^n{\frac{4k}{{4{k^2}-1}}}，（{n∈{N_+}}）$．
3．设a，b，c为互不相等的正数，则下列不等式不一定成立的是（　　）
A．|a-b|≤|a|+|b|B．|a-b|≤|a-c|+|b-c|C．$\frac{b}{a}$＜$\frac{b+c}{a+c}$D．a2+$\frac{1}{{a}^{2}}$≥a+$\frac{1}{a}$
20．数列{an}满足a1+2a2+…+nan=4-$\frac{n+2}{{{2^{n-1}}}}$，n∈N*．
（1）求a3的值；
（2）求数列{an}的通项公式；
（3）设${b_n}=1+{log_{\frac{1}{2}}}{a_n}$，求证：$\frac{1}{b_1^2}+\frac{1}{b_2^2}+…+\frac{1}{b_n^2}＜\frac{7}{4}$．
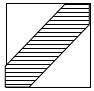1．如图，在边长为25cm的正方形中挖去边长为18cm的两个等腰直角三角形，现有均匀的粒子散落在正方形中，问粒子落在中间带形区域的概率是多少$\frac{301}{625}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网