题目内容
13.设数列{an}的前n项和为Sn,满足(3-m)Sn+2man=m+3(n∈N*).其中m为常数,且m≠-3,m≠0.(1)求证:数列{an}是等比数列.
(2)若数列{an}的公比q=f(m),数列{bn}满足b1=a1,bn=$\frac{3}{2}$f(bn-1)(n∈N*,n≥2),求证:数列{$\frac{1}{{b}_{n}}$}为等差数列.
分析 (1)求得n=1时,a1=S1=1,由an+1=Sn+1-Sn,将n换为n+1,相减,结合等比数列的定义,即可得到证明;
(2)求得b1=a1=1,由(1)可得q=f(m),由题意可得bnbn-1+3bn=3bn-1,整理可得,$\frac{1}{{b}_{n}}$-$\frac{1}{{b}_{n-1}}$=$\frac{1}{3}$,运用等差数列的定义,即可得证.
解答 证明:(1)由n=1可得a1=S1,即有(3-m)S1+2ma1=m+3,解得a1=1,
由an+1=Sn+1-Sn,
(3-m)Sn+2man=m+3,得(3-m)Sn+1+2man+1=m+3,
两式相减得(3+m)an+1=2man,
因为m≠0且m≠-3,所以$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{2m}{m+3}$,
所以数列{an}是首项为1,公比为$\frac{2m}{m+3}$的等比数列;
(2)因为b1=a1=1,q=f(m)=$\frac{2m}{m+3}$,
所以n∈N*且n≥2时,bn=$\frac{3}{2}$f(bn-1)=$\frac{3}{2}$•$\frac{2{b}_{n-1}}{3+{b}_{n-1}}$,
可得bnbn-1+3bn=3bn-1,$\frac{1}{{b}_{n}}$-$\frac{1}{{b}_{n-1}}$=$\frac{1}{3}$,
所以数列{$\frac{1}{{b}_{n}}$}是以1为首项,$\frac{1}{3}$为公差的等差数列.
点评 本题考查等差数列和等比数列的定义的运用,考查数列递推式的运用,考查转化思想,化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
8.己知将函数f(x)=$\sqrt{3}$sinxcosx+cos2x-$\frac{1}{2}$的图象向左平移$\frac{5π}{12}$个单位长度后得到y=g(x)的图象,则g(x)在[-$\frac{π}{12}$,$\frac{π}{3}$]上的值域为( )
| A. | [-$\frac{1}{2}$,1] | B. | [-1,$\frac{1}{2}$] | C. | [-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$] | D. | [-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |
2.a,b,c是△ABC中角A,B,C的对边,则直线sinAx+ay+c=0与sinBx+by=0的位置关系是( )
| A. | 相交 | B. | 重合 | C. | 垂直 | D. | 平行 |
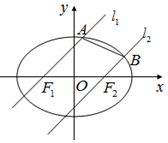 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为F1、F2,离心率为$\frac{1}{2}$,直线y=1与C的两个交点间的距离为$\frac{{4\sqrt{6}}}{3}$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右焦点分别为F1、F2,离心率为$\frac{1}{2}$,直线y=1与C的两个交点间的距离为$\frac{{4\sqrt{6}}}{3}$. 如图所示,Rt△ABC的顶点A坐标(-2,0),直角顶点B(0,-2$\sqrt{2}$),顶点C在x轴上,点P为线段OA的中点.
如图所示,Rt△ABC的顶点A坐标(-2,0),直角顶点B(0,-2$\sqrt{2}$),顶点C在x轴上,点P为线段OA的中点.