题目内容
3.已知函数y=2cosx的定义域为$[\frac{π}{3},π]$,值域为[a,b],(Ⅰ)求a,b的值;
(Ⅱ)求函数y=asinx+b的最值及取得最值时x的值.
分析 (Ⅰ)利用余弦函数的单调性,即可求a,b的值;
(Ⅱ)利用正弦函数的最值,即可求函数y=asinx+b的最值及取得最值时x的值.
解答 解:(Ⅰ)∵函数y=2cosx的定义域为$[\frac{π}{3},π]$,值域为[a,b],
∴2cos$\frac{π}{3}$=b,2cosπ=a,
∴a=-2,b=1;
(Ⅱ)函数y=asinx+b=-2sinx+1,
∴sinx=1,即x=2kπ+$\frac{π}{2}$(k∈Z)时,y=-2sinx+1的最小值为-1;
sinx=-1,即x=2kπ-$\frac{π}{2}$(k∈Z)时,y=-2sinx+1的最大值为3.
点评 本题考查三角函数的图象与性质,考查学生的计算能力,属于中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
14.表面积为20π的球面上有四点S、A、B、C,且△ABC是边长为2$\sqrt{3}$的等边三角形,若平面SAB⊥平面ABC,则三棱锥S-ABC体积的最大值是( )
| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | 4$\sqrt{3}$ |
8.设a<0,角α的终边经过点P(3a,-4a),则sinα+2cosα的值等于( )
| A. | $\frac{2}{5}$ | B. | $-\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $-\frac{1}{5}$ |
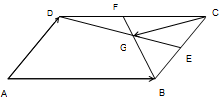 如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量
如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量