Question

3．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右焦点分别为F₁、F₂，离心率为$\frac{1}{2}$，直线y=1与C的两个交点间的距离为$\frac{{4\sqrt{6}}}{3}$．
（Ⅰ）求椭圆C的方程；
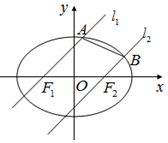
（Ⅱ）分别过F₁、F₂作l₁、l₂满足l₁∥l₂，设l₁、l₂与C的上半部分分别交于A、B两点，求四边形ABF₂F₁面积的最大值．

Answer 1

分析 （Ⅰ）利用离心率为$\frac{1}{2}$，直线y=1与C的两个交点间的距离为$\frac{{4\sqrt{6}}}{3}$，求出a，b，即可求椭圆C的方程；
（Ⅱ）直线与椭圆方程联立，利用基本不等式，求四边形ABF₂F₁面积的最大值．

解答 解：（Ⅰ）易知椭圆过点$（\frac{{2\sqrt{6}}}{3}，1）$，所以$\frac{8}{{3{a^2}}}+\frac{1}{b^2}=1$，①…（2分）
又$\frac{c}{a}=\frac{1}{2}$，②…（3分）a²=b²+c²，③…（4分）
①②③得a²=4，b²=3，
所以椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$．…（6分）
（Ⅱ）设直线l₁：x=my-1，它与C的另一个交点为D．
与C联立，消去x，得（3m²+4）y²-6my-9=0，…（7分）
△=144（m²+1）＞0.$|{AD}|=\sqrt{1+{m^2}}•\frac{{12\sqrt{1+{m^2}}}}{{3{m^2}+4}}$，…（9分）
又F₂到l₁的距离为$d=\frac{2}{{\sqrt{1+{m^2}}}}$，…（10分）
所以${S_{△AD{F_2}}}=12\frac{{\sqrt{1+{m^2}}}}{{3{m^2}+4}}$．…（11分）
令$t=\sqrt{1+{m^2}}≥1$，则${S_{△AD{F_2}}}=\frac{12}{{3t+\frac{1}{t}}}$，所以当t=1时，最大值为3．…（14分）
又${S_{四边形AB{F_2}{F_1}}}=\frac{1}{2}（|{B{F_2}}|+|{A{F_1}}|）•d=\frac{1}{2}（|{A{F_1}}|+|{D{F_1}}|）•d=\frac{1}{2}|{AB}|•d={S_{△AD{F_2}}}$
所以四边形ABF₂F₁面积的最大值为3．                …（15分）

点评 本题考查椭圆的方程与性质，考查直线与椭圆位置关系的运用，考查面积的计算，属于中档题．