题目内容
8.己知将函数f(x)=$\sqrt{3}$sinxcosx+cos2x-$\frac{1}{2}$的图象向左平移$\frac{5π}{12}$个单位长度后得到y=g(x)的图象,则g(x)在[-$\frac{π}{12}$,$\frac{π}{3}$]上的值域为( )| A. | [-$\frac{1}{2}$,1] | B. | [-1,$\frac{1}{2}$] | C. | [-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$] | D. | [-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] |
分析 利用三角函数的恒等变换化简函数的解析式,再利用函数y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再来一用正弦函数的定义域和值域,求得g(x)在[-$\frac{π}{12}$,$\frac{π}{3}$]上的值域.
解答 解:将函数f(x)=$\sqrt{3}$sinxcosx+cos2x-$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x=sin(2x+$\frac{π}{6}$)
的图象向左平移$\frac{5π}{12}$个单位长度后,
得到y=g(x)=sin(2x+$\frac{5π}{6}$+$\frac{π}{6}$)=sin(2x+π)=-sin2x 的图象,
在[-$\frac{π}{12}$,$\frac{π}{3}$]上,2x∈[-$\frac{π}{6}$,$\frac{2π}{3}$],-sin2x∈[-1,$\frac{1}{2}$],
则g(x)在[-$\frac{π}{12}$,$\frac{π}{3}$]上的值域为[-1,$\frac{1}{2}$],
故选:B.
点评 本题主要考查三角函数的恒等变换,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的定义域和值域,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列函数中,在(0,$\frac{π}{2}$)上是增函数的偶函数是( )
| A. | y=|sinx| | B. | y=|sin2x| | C. | y=|cosx| | D. | y=tanx |
 已知圆O:x2+y2=4及一点P(-1,0),Q在圆O上运动一周,PQ的中点M形成轨迹C.
已知圆O:x2+y2=4及一点P(-1,0),Q在圆O上运动一周,PQ的中点M形成轨迹C. 如图,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )
如图,设点A是单位圆上的一定点,动点P从点A出发在圆上按逆时针方向旋转一周,点P所旋转过的弧的长为l,弦AP的长为d,则函数d=f(l)的图象大致是( )



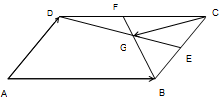 如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量
如图,在平行四边形ABCD中,E、F分别为BC与DC中点,G为BF与DE交点,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a$,$\overrightarrow b$为基底表示下面向量