题目内容
已知二次函数f(x)=ax2+bx+c,函数g(x)=f(x)-
[f(1)+f(3)],若a>0且f(x-1)=f(-x-1),g(x)在区间[-2,2]上最大值为-1,求g(x)的表达式.
| 1 |
| 2 |
考点:二次函数的性质
专题:函数的性质及应用
分析:由已知中a>0且f(x-1)=f(-x-1),可得函数f(x),g(x)的图象关于直线x=-
=-1对称;结合g(x)在区间[-2,2]上最大值为-1,构造方程求出a,b值,代入可得g(x)的表达式.
| b |
| 2a |
解答:
解:∵二次函数f(x)=ax2+bx+c满足f(x-1)=f(-x-1),
故函数f(x),g(x)的图象关于直线x=-
=-1对称,即b=2a,
又∵a>0,
故在区间[-2,2]上,
当x=2,g(x)max=f(2)-
[f(1)+f(3)]=4a+2b+c-
[(a+b+c)+(9a+3b+c)]=-a=-1
解得a=1,b=2
∴f(x)=x2+2x+c,
∴f(1)=3+c,f(3)=15+c,
∴g(x)=f(x)-
[f(1)+f(3)]
=x2+2x+c-
(3+c+15+c)
=x2+2x-9,
即g(x)=x2+2x-9.
故函数f(x),g(x)的图象关于直线x=-
| b |
| 2a |
又∵a>0,
故在区间[-2,2]上,
当x=2,g(x)max=f(2)-
| 1 |
| 2 |
| 1 |
| 2 |
解得a=1,b=2
∴f(x)=x2+2x+c,
∴f(1)=3+c,f(3)=15+c,
∴g(x)=f(x)-
| 1 |
| 2 |
=x2+2x+c-
| 1 |
| 2 |
=x2+2x-9,
即g(x)=x2+2x-9.
点评:本题考查的知识点是二次函数的性质,其中根据已知分析出函数的对称性,进而构造关于a,b的方程是解答的关键.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
若函数f(x)同时具有以下两个性质:①f(x)是偶函数,②对任意实数x,都有f(
+x)=f(
-x),则f(x)的解析式可以是( )
| π |
| 4 |
| π |
| 4 |
| A、f(x)=cosx | ||
B、f(x)=cos(2x+
| ||
C、f(x)=sin(4x+
| ||
| D、f(x)=cos6x |
一个算法的程序框图如图所示,如果输入的x的值为2014,则输出的i的结果为( )
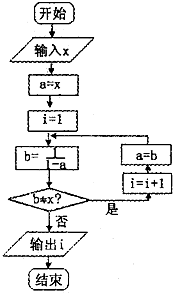

| A、3 | B、5 | C、6 | D、8 |