题目内容
已知直线l:ax-y=0在矩阵A=
对应的变换作用下得到直线l′,若直线l′过点(1,1),求实数a= .
|
考点:变换、矩阵的相等
专题:选作题,矩阵和变换
分析:设直线l:ax-y=0上任意一点(x,y),在矩阵A=
对应的变换作用下得到(x′,y′),根据矩阵变换特点,写出两对坐标之间的关系,把已知的点的坐标代入得到直线的方程,得到结果.
|
解答:
解:设直线l上的点(x,y),(x′,y′)是所得的直线上一点,则
=
∴
,
令x′=1,y′=1,则x=-1,y=1,
代入ax-y=0,可得a=-1.
故答案为:-1.
|
|
|
∴
|
令x′=1,y′=1,则x=-1,y=1,
代入ax-y=0,可得a=-1.
故答案为:-1.
点评:本题主要考查二阶矩阵的变换,考查运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设a=log37,b=23.3,c=0.8,则( )
| A、b<a<c |
| B、c<a<b |
| C、c<b<a |
| D、a<c<b |
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=
,则φ的值为( )
| π |
| 8 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
 如图,AB,CD是半径为1的圆O的两条弦,它们相交于AB的中点P,PD=
如图,AB,CD是半径为1的圆O的两条弦,它们相交于AB的中点P,PD=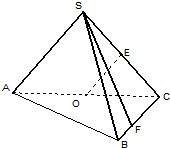 如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=