题目内容
曲线y=
在点(0,0)处的切线方程为( )
| x |
| x+2 |
| A、y=2x | ||
| B、y=2x-2 | ||
C、y=
| ||
D、y=
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:根据导数的几何意义求出函数在x=0处的导数,从而得到切线的斜率,再利用点斜式方程写出切线方程即可.
解答:
解:∵y=
,
∴y'=
,
∴x=0时,y'=
,
∴曲线y=
在点(0,0)处的切线方程为y=
x.
故选:C.
| x |
| x+2 |
∴y'=
| 2 |
| (x+2)2 |
∴x=0时,y'=
| 1 |
| 2 |
∴曲线y=
| x |
| x+2 |
| 1 |
| 2 |
故选:C.
点评:本题主要考查了利用导数研究曲线上某点切线方程,考查运算求解能力,属于基础题.

练习册系列答案
相关题目
设a=log37,b=23.3,c=0.8,则( )
| A、b<a<c |
| B、c<a<b |
| C、c<b<a |
| D、a<c<b |
设点P在曲线ρsinθ=2上,点Q在曲线ρ=-2cosθ上,则|PQ|的最小值为( )
| A、2 | B、1 | C、3 | D、0 |
设x,y∈R,则“x≥2,且y≥2”是“x2+y2≥8”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
在极坐标系中,点(2,
)到直线ρ(
cosθ+sinθ)=2的距离为( )
| π |
| 6 |
| 3 |
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=
,则φ的值为( )
| π |
| 8 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
在空间直角坐标系中,点P(3,-2,1)关于y对称的点的坐标是( )
| A、(3,2,-1) |
| B、(-3,-2,-1) |
| C、(-3,2,-1) |
| D、(-3,2,-1) |
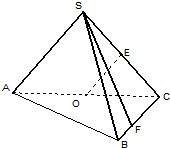 如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=
如图,在三棱锥S-ABC中,侧面SAC与底面ABC垂直,E,O分别是SC,AC的中点,SA=SC=