题目内容
若a>0,b>0且4a2+b2=4,则a
的最大值是( )
| 1+b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:基本不等式
专题:不等式的解法及应用
分析:变形利用基本不等式的性质即可得出:a
=
•2a
≤
.
| 1+b2 |
| 1 |
| 2 |
| 1+b2 |
| 1 |
| 2 |
| 4a2+(1+b2) |
| 2 |
解答:
解:∵a>0,b>0且4a2+b2=4,∴4a2+(1+b2)=5.
∴a
=
•2a
≤
=
,当且仅当4a2=1+b2=
时取等号.
故选:C.
∴a
| 1+b2 |
| 1 |
| 2 |
| 1+b2 |
| 1 |
| 2 |
| 4a2+(1+b2) |
| 2 |
| 5 |
| 4 |
| 5 |
| 2 |
故选:C.
点评:本题考查了基本不等式的性质,属于基础题.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)图象的一条对称轴是直线x=
,则φ的值为( )
| π |
| 8 |
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
在空间直角坐标系中,点P(3,-2,1)关于y对称的点的坐标是( )
| A、(3,2,-1) |
| B、(-3,-2,-1) |
| C、(-3,2,-1) |
| D、(-3,2,-1) |
将点P(-2,2)变换为P′(-6,1)的伸缩变换公式为( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
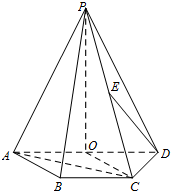 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,CD⊥平面PAD,BC∥AD,PA=PD,O,E分别为AD,PC的中点,PO=AD=2BC=2CD.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,CD⊥平面PAD,BC∥AD,PA=PD,O,E分别为AD,PC的中点,PO=AD=2BC=2CD.