题目内容
为了得到函数y=
(sin2x-cos2x)的图象,只要把函数y=sin2x的图象上所有的点( )
| ||
| 2 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:利用三角恒等变换的应用,可求得y=
(sin2x-cos2x)=sin[2(x-
)],再利用函数y=Asin(ωx+φ)的图象变换即可求得答案.
| ||
| 2 |
| π |
| 8 |
解答:
解:∵y=
(sin2x-cos2x)
=
×
(
sin2x-
cos2x)
=sin(2x-
)
=sin[2(x-
)],
∴要得到函数y=
(sin2x-cos2x)=sin(2x-
)的图象,只需把函数y=sin2x的图象上所有的点向右平行移动
个单位即可.
故选:D.
| ||
| 2 |
=
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
=sin(2x-
| π |
| 4 |
=sin[2(x-
| π |
| 8 |
∴要得到函数y=
| ||
| 2 |
| π |
| 4 |
| π |
| 8 |
故选:D.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,考查三角恒等变换的应用,属于中档题.

练习册系列答案
相关题目
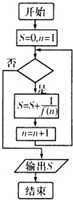
已知函数 f(x)=x2+x,执行如图所示的程序框图,若输出的结果是
,则判断框中的条件应是( )
| 31 |
| 32 |

| A、n≤30 | B、n≤31 |
| C、n≤32 | D、n≤33 |
定义在R上的函数f(x)的图象既关于点(1,1)对称,又关于点(3,2)对称,则f(0)+f(2)+f(4)+…+f(18)=( )
| A、24 | B、32 | C、46 | D、50 |
已知复数z满足:iz=3+4i(i为虚数单位),则z的共轭复数在复平面内对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若tanα=3,则cos2α等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|

