题目内容
假设在时间间隔T内的任何时刻，两条不相关的短信机会均等地进入同一台手机．若这两条短信进入手机的间隔时间不大于t（0＜t＜T）称手机受到干扰，则手机受到干扰的概率是（ ）
A、（
| ||
B、（1-
| ||
C、1-（
| ||
D、1-（1-
|
考点：几何概型
专题：概率与统计
分析：根据几何概型的概率公式求出对应的测度，即可得到结论．
解答：
分别设两个互相独立的短信收到的时间为x，y．则所有事件集可表示为0≤x≤T，0≤y≤T．
由题目得，如果收音机受则到干扰的事件发生，必有|x-y|≤t．
三个不等式联立，则该事件即为
x-y=t 和 y-x=t 在 0≤x≤T，0≤y≤T 的正方形中围起来的图形．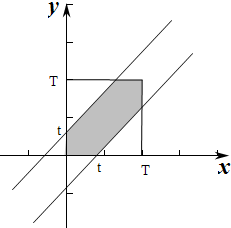
即图中阴影区域
而所有事件的集合即为正方型面积T2，
阴影部分的面积T2-2×
(T-t)2=T2-（T-t）2，
所以阴影区域面积和正方形面积比值即为干扰发生的概率
为
=1-（1-
）2，
故选：D
由题目得，如果收音机受则到干扰的事件发生，必有|x-y|≤t．
三个不等式联立，则该事件即为
x-y=t 和 y-x=t 在 0≤x≤T，0≤y≤T 的正方形中围起来的图形．
即图中阴影区域
而所有事件的集合即为正方型面积T2，
阴影部分的面积T2-2×
| 1 |
| 2 |
所以阴影区域面积和正方形面积比值即为干扰发生的概率
为
| T2-(T-t)2 |
| T2 |
| t |
| T |
故选：D
点评：本题主要考查几何概型的概率的计算，分别求出对应区域的面积是解决本题的关键，比较基础．
练习册系列答案
相关题目
已知向量
、
满足|
|=1，|
|=
，且（3
-2
）⊥
，则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
命题p：x∈R且满足sin2x=1．命题q：x∈R且满足tanx=1．则p是q的（ ）
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
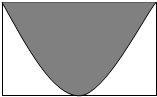如图，长方形的面积为2，将100颗豆子随机地撒在长方形内，其中恰好有60颗豆子落在阴影部分内，则用随机摸拟的方法可以估计图中阴影部分的面积为（ ）
如图所示，一游泳者自游泳池边AB上的D点，沿DC方向游了10米，∠CDB=60°，然后任意选择一个方向并沿此方向继续游，则他再游不超过10米就能够回到游泳池AB边的概率是（ ）