题目内容
从5双不同颜色的手套中任取4只,其中恰好有一双同色的取法有( )
| A、120 | B、240 |
| C、360 | D、72 |
考点:等可能事件的概率
专题:概率与统计
分析:根据分步计数原理知先从5双手套中任选一双,再从其余手套中任选2只,其中包含选到一双同色手套的选法,把不合题意的去掉,得到总的选法数.
解答:
解:根据分步计数原理知
先从5双手套中任选一双有C51种取法,
再从其余手套中任选2只有C82种,
其中选到一双同色手套的选法为
种.
故总的选法数为C51(C82-
)=120种.
故选:A.
先从5双手套中任选一双有C51种取法,
再从其余手套中任选2只有C82种,
其中选到一双同色手套的选法为
| C | 1 4 |
故总的选法数为C51(C82-
| C | 1 4 |
故选:A.
点评:手套和袜子成对问题是一种比较困难的题目,解决组合问题要做到不重不漏,有些题目带有一定的约束条件,解题时要先考虑有限制条件的元素.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
执行如图的程序框图,则输出的S的值为( )


| A、1 | B、2 | C、3 | D、4 |
已知sinθ-cosθ=
,则sin2θ的值是( )
| 1 |
| 5 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
物体自由落体运动方程为s(t)=
gt2,若
=g=9.8m/s,那么下面说法正确的是( )
| 1 |
| 2 |
| lim |
| n→∞ |
| s(1+△t)-s(1) |
| △t |
| A、9.8m/s是0~1s这段时间内的平均速度 |
| B、9.8m/s是从1s到(1+△t)s这段时间内的速度 |
| C、9.8m/s是物体在t=1s这一时刻的速度 |
| D、9.8m/s是物体从1s到(1+△t)s这段时间内的平均速度 |
设a,b∈R,则“(a-b)3b2>0”是“a>b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
常说“便宜没好货”,这句话的意思是:“不便宜”是“好货”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
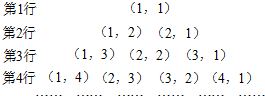 把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.
把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.