题目内容
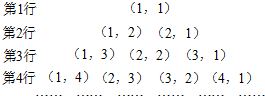 把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.
把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.(1)a64表示的数对为
(2)已知aij对应的数对为(2m,n)(m,n为正整数),则i+j=
考点:归纳推理
专题:推理和证明
分析:由前4行得到,每一行的第一个数对是(1,n),n为行数,接着的每一个数对前一个数是连续的自然数,后一个是依次减1的数,由此推出第n行的数对,即可得到(1)、(2)的结论,注意每一行中,第一个数是列数,两个数之和减1是行数.
解答:
解:由前4行的特点:每一行的第一个数对是(1,n),n为行数,
接着的每一个数对前一个数是连续的自然数,后一个是依次减1的数,
可得,第n行可为:(1,n),(2,n-1),(3,n-2),…,(n-1,2),(n,1).
(1)a64表示的数对为(4,3);
(2)由aij对应的数对为(2m,n)(m,n为正整数),得,i=2m+n-1,j=2m,故i+j=4m+n-1.
故答案为:(4,3),4m+n-1.
接着的每一个数对前一个数是连续的自然数,后一个是依次减1的数,
可得,第n行可为:(1,n),(2,n-1),(3,n-2),…,(n-1,2),(n,1).
(1)a64表示的数对为(4,3);
(2)由aij对应的数对为(2m,n)(m,n为正整数),得,i=2m+n-1,j=2m,故i+j=4m+n-1.
故答案为:(4,3),4m+n-1.
点评:本题主要考查归纳推理的思想方法,注意观察和分析数对的特点,是解决该类问题的关键.

练习册系列答案
相关题目
已知向量
=(2,4)与向量
=(-4,y)垂直,则y=( )
| a |
| b |
| A、-2 | B、-1 | C、1 | D、2 |
将-330°化为弧度为( )
A、-
| ||
B、-
| ||
C、-
| ||
D、
|
从5双不同颜色的手套中任取4只,其中恰好有一双同色的取法有( )
| A、120 | B、240 |
| C、360 | D、72 |
已知集合A={x|m+1≤x≤2m},B={x|log2x≤3},当A∩B=∅时,实数m的取值范围是( )
| A、1<m<7 |
| B、m<1或m>7 |
| C、0≤m<7 |
| D、m≤0或m>7 |