题目内容
设a，b∈R，则“（a-b）3b2＞0”是“a＞b”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式之间的关系，利用充分条件和必要条件的定义进行判断即可．
解答：
解：因为（a-b）3b2＞0?a＞b，b≠0，显然（a-b）3b2＞0⇒a＞b，反之不成立，
故选：A．
故选：A．
点评：本题考查充分必要条件的判断，根据不等式的性质是解决本题的关键，比较基础．
练习册系列答案
相关题目
从5双不同颜色的手套中任取4只，其中恰好有一双同色的取法有（ ）
| A、120 | B、240 |
| C、360 | D、72 |
若sinα=
，则cos2α等于（ ）
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列命题正确的是（ ）
A、若
| ||||||||
B、若
| ||||||||
C、向量
| ||||||||
| D、两向量相等的充要条件是它们的始点、终点相同 |
如图网格中的图形为某个多面体的三视图，每个小正方形的边长为1，则该多面体的外接圆的表面积为（ ）| A、3π | ||
B、32
| ||
| C、48π | ||
| D、192π |
已知集合A={x|m+1≤x≤2m}，B={x|log2x≤3}，当A∩B=∅时，实数m的取值范围是（ ）
| A、1＜m＜7 |
| B、m＜1或m＞7 |
| C、0≤m＜7 |
| D、m≤0或m＞7 |
如果执行如图所示的程序框图，输入正整数N（N≥2）和实数a1，a2，…，an，输出A，B，则（ ）
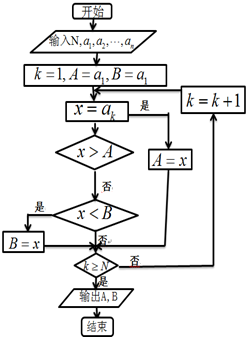
| A、A和B分别是a1，a2，…，an中最小的数和最大的数 | ||
| B、A和B分别是a1，a2，…，an中最大的数和最小的数 | ||
C、
| ||
| D、A+B为a1，a2，…，an的和 |