题目内容
2.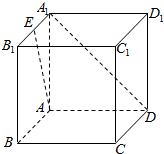 如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.
如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.
分析 以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AE与A1D所成的角的余弦值.
解答 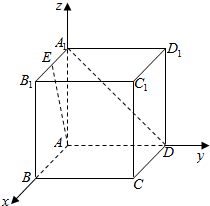 解:以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
解:以A为原点,AB为x轴,AD为y轴,AA1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1中棱长为2,
则A(0,0,0),E(1,0,2),A1(0,0,2),D(0,2,0),
$\overrightarrow{AE}$=(1,0,2),$\overrightarrow{{A}_{1}D}$=(0,2,-2),
设异面直线AE与A1D所成的角为θ,
则cosθ=|cos<$\overrightarrow{AE}$,$\overrightarrow{{A}_{1}D}$>|=$\frac{|\overrightarrow{AE}•\overrightarrow{{A}_{1}D}|}{|\overrightarrow{AE}|•|\overrightarrow{{A}_{1}D}|}$=$\frac{|-4|}{\sqrt{5}•\sqrt{8}}$=$\frac{\sqrt{10}}{5}$.
∴异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.
故答案为:$\frac{\sqrt{10}}{5}$.
点评 本题考查异面直线所成角的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
12.在直三棱柱ABC-A1B1C1中,AC=AA1=2,∠ACB=90°,点E,F分别是棱AB,BB1的中点,当二面角C1-AA1-B为45°时,直线EF与BC1的夹角为( )
| A. | 60° | B. | 45° | C. | 90° | D. | 120° |
13.设Sn为等差数列{an}的前n项和,若已知S6<S7,S7>S8,则下列叙述中正确的个数有( )
①S7是所有Sn(n∈N*)中的最大值;
②a7是所有an(n∈N*)中的最大值;
③公差d一定小于0;
④S9一定小于S6.
①S7是所有Sn(n∈N*)中的最大值;
②a7是所有an(n∈N*)中的最大值;
③公差d一定小于0;
④S9一定小于S6.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.若集合 A={x|-3<x<3},B={x|(x+4)(x-2)>0},则 A∩B=( )
| A. | {x|-3<x<2} | B. | {x|2<x<3} | C. | {x|-3<x<-2} | D. | {x|x<-4或x>-3} |
7.“m=1”是“直线mx-y=0和直线x+m2y=0互相垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |