题目内容
13.设Sn为等差数列{an}的前n项和,若已知S6<S7,S7>S8,则下列叙述中正确的个数有( )①S7是所有Sn(n∈N*)中的最大值;
②a7是所有an(n∈N*)中的最大值;
③公差d一定小于0;
④S9一定小于S6.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用等差数列的性质求解.
解答 解:∵a7>0,a8<0,∴S7最大,故①正确;
∵d<0,∴a1最大,故②错误;
由s6<s7,S7>S8可得S7-S6=a7>0,S8-S7=a8<0
∴a8-a7=d<0,故③正确;
S9-S6=a7+a8+a9=3a8<0,故④正确.
故选:C.
点评 本题考查命题真假的判断,是基础题,解题时要认真审题,注意数列的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知集合A={1,2,3},B={2,3,4,5},全集U={1,2,3,4,5,6},则∁U(A∩B)=( )
| A. | {2,3} | B. | {1,4,5} | C. | {1,4,5,6} | D. | {1,2,3,4,5} |
18.下列说法中正确的是( )
| A. | 若a>b,则ac2>bc2 | |
| B. | 若x≠0,则x+$\frac{4}{x}$的最小值为4 | |
| C. | “φ=$\frac{π}{2}$”是函数y=sin(x+φ)为偶函数“的充要条件 | |
| D. | 命题“?x>0,x-lnx>0”的否定是“?x0>0,x0-lnx0≤0” |
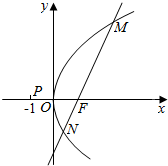 已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.
已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.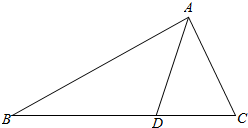 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.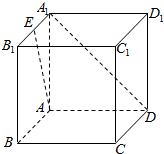 如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.
如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.