题目内容
12．定义在R上的奇函数y=f（x）满足f（x+2）=f（-x），则f（-2008）=0．分析 根据函数奇偶性以及函数关系，判断函数的周期性进行求解即可．
解答 解：∵定义在R上的奇函数y=f（x）满足f（x+2）=f（-x），
∴f（x+2）=f（-x）=-f（x），
即f（x+4）=-f（x+2）=f（x），
即函数的周期是4，
∵f（x）是奇函数，∴f（0）=0，
则f（-2008）=f（-502×4）=f（0）=0，
故答案为：0
点评 本题主要考查函数值的计算，根据条件判断函数的周期性，利用函数的周期性进行转化求解是解决本题的关键．
练习册系列答案
相关题目
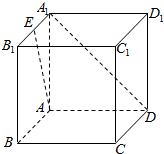如图，在正方体ABCD-A1B1C1D1中，E为A1B1的中点，则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$．