题目内容
12.在直三棱柱ABC-A1B1C1中,AC=AA1=2,∠ACB=90°,点E,F分别是棱AB,BB1的中点,当二面角C1-AA1-B为45°时,直线EF与BC1的夹角为( )| A. | 60° | B. | 45° | C. | 90° | D. | 120° |
分析 先将EF平移到AB1,再利用中位线进行平移,使两条异面直线移到同一点,得到直线EF和BC1所成的角,求之即可.
解答  解:由题意可得∠CAB=45°为二面角C1-AA1-B的平面角,△ABC为等腰直角三角形,
解:由题意可得∠CAB=45°为二面角C1-AA1-B的平面角,△ABC为等腰直角三角形,
连AC1,取AC1得中点O,∵E,F分别是棱AB,BB1的中点,∴OE平行且等于$\frac{1}{2}$BC1,
∠OEF=θ或其补角,即为直线EF与BC1的夹角.
由于OE=$\frac{1}{2}$BC1=$\sqrt{2}$,EF=$\sqrt{{BF}^{2}{+EB}^{2}}$=$\sqrt{1+2}$=$\sqrt{3}$,OF=$\sqrt{{2}^{2}+1}$=$\sqrt{5}$,
由余弦定理可得cosθ=$\frac{{OE}^{2}{+EF}^{2}{-OF}^{2}}{2OE•EF}$=0,
∴θ=90°,
故选:C.
点评 本题主要考查了异面直线及其所成的角,平移法是研究异面直线所成的角的最常用的方法,经常考查,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
2.已知a=1.7-2.5,b=2.51.7,c=${log_2}{\frac{2}{3}}$,则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
17.${(x-\frac{2}{x^2})^6}$展开式中的常数项为( )
| A. | 60 | B. | -60 | C. | 30 | D. | -30 |
4.已知集合A={1,2,3},B={2,3,4,5},全集U={1,2,3,4,5,6},则∁U(A∩B)=( )
| A. | {2,3} | B. | {1,4,5} | C. | {1,4,5,6} | D. | {1,2,3,4,5} |
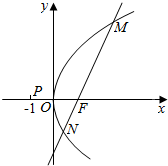 已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.
已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.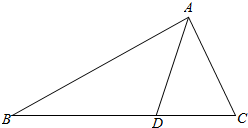 如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.
如图,在△ABC中,点D在BC边上,∠CAD=$\frac{π}{4}$,AC=$\frac{7}{2}$,cos∠ADB=-$\frac{{\sqrt{2}}}{10}$.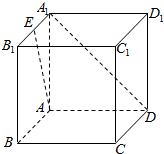 如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.
如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.