题目内容
7.“m=1”是“直线mx-y=0和直线x+m2y=0互相垂直”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合直线垂直的等价条件进行判断即可.
解答 解:若m=1,则两直线方程为x-y=0和x+y=0,满足垂直,
当m=0时,两直线方程为-y=0和x=0,满足垂直,但m=1不成立,
即“m=1”是“直线mx-y=0和直线x+m2y=0互相垂直”的充分不必要条件,
故选:A.
点评 本题主要考查充分条件和必要条件的判断,结合直线垂直的条件是解决本题的关键.

练习册系列答案
相关题目
17.${(x-\frac{2}{x^2})^6}$展开式中的常数项为( )
| A. | 60 | B. | -60 | C. | 30 | D. | -30 |
18.下列说法中正确的是( )
| A. | 若a>b,则ac2>bc2 | |
| B. | 若x≠0,则x+$\frac{4}{x}$的最小值为4 | |
| C. | “φ=$\frac{π}{2}$”是函数y=sin(x+φ)为偶函数“的充要条件 | |
| D. | 命题“?x>0,x-lnx>0”的否定是“?x0>0,x0-lnx0≤0” |
15.若x,y满足$\left\{\begin{array}{l}x-y+3≥0\\ x+y+1≥0\\ x≤k\end{array}\right.$且z=2x+y的最大值为6,则k的值为( )
| A. | -1 | B. | 1 | C. | -7 | D. | 7 |
19.设公差不为零的等差数列{an}的前n项和为Sn,若a4=2(a2+a3),则$\frac{{S}_{2}}{{S}_{4}}$=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{14}{5}$ | C. | 7 | D. | 14 |
16.函数y=$\frac{1}{x}ln[\sqrt{{x^2}-3x+2}+\sqrt{-{x^2}-3x+4}]$的定义域是( )
| A. | [-4,0)∪(0,1) | B. | [-4,0)∪(0,1] | C. | (-4,0)∪(0,1) | D. | (-∞,-4)∪[2,+∞) |
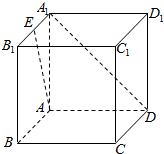 如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.
如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.