题目内容
14.已知数列$\frac{1}{1×3}$,$\frac{1}{3×5}$,$\frac{1}{5×7}$,…,$\frac{1}{(2n-1)(2n+1)}$,…的前n项和为Sn,计算得S1=$\frac{1}{3}$,S2=$\frac{2}{5}$,S3=$\frac{3}{7}$,照此规律,Sn=$\frac{n+1}{2}$.分析 由已知条件利用裂项求和法求解.
解答 解:∵数列$\frac{1}{1×3}$,$\frac{1}{3×5}$,$\frac{1}{5×7}$,…,$\frac{1}{(2n-1)(2n+1)}$,…的前n项和为Sn,
∴S1=$\frac{1}{1×3}$=$\frac{1}{2}(1-\frac{1}{3})$=$\frac{1}{3}$,
S2=$\frac{1}{1×3}+\frac{1}{3×5}$=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}-\frac{1}{5}$)=$\frac{2}{5}$,
S3=$\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}$=$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7})$=$\frac{3}{7}$,
照此规律,Sn=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{(2n-1)(2n+1)}$
=$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$
=$\frac{1}{2}(1-\frac{1}{2n+1})$
=$\frac{n}{2n+1}$.
故答案为:$\frac{n}{2n+1}$.
点评 本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
相关题目
4.已知集合A={1,2,3},B={2,3,4,5},全集U={1,2,3,4,5,6},则∁U(A∩B)=( )
| A. | {2,3} | B. | {1,4,5} | C. | {1,4,5,6} | D. | {1,2,3,4,5} |
19.设公差不为零的等差数列{an}的前n项和为Sn,若a4=2(a2+a3),则$\frac{{S}_{2}}{{S}_{4}}$=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{14}{5}$ | C. | 7 | D. | 14 |
6.设a>b,则下列不等式成立的是( )
| A. | a2+b2>ab | B. | $\frac{b-a}{ab}$<0 | C. | a2>b2 | D. | 2a<2b |
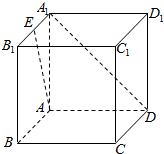 如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$.
如图,在正方体ABCD-A1B1C1D1中,E为A1B1的中点,则异面直线AE与A1D所成的角的余弦值为$\frac{\sqrt{10}}{5}$. 执行如图所示的程序框图,设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出的S的值为n,则m+n=14.
执行如图所示的程序框图,设当箭头a指向①处时,输出的S的值为m,当箭头a指向②处时,输出的S的值为n,则m+n=14.