题目内容
4.如果函数f(x)=sinωx+$\sqrt{3}$cosωx的两个相邻零点间的距离为2,那么f(1)+f(2)+f(3)+…+f(9)的值为( )| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
分析 化简函数f(x),根据f(x)的图象两个相邻零点间的距离为2得出f(x)的最小正周期为4,
求出ω的值,再计算f(1)+f(2)+f(3)+…+f(9)的值.
解答 解:函数f(x)=sinωx+$\sqrt{3}$cosωx=2sin(ωx+$\frac{π}{3}$),
且f(x)的图象两个相邻零点间的距离为2,
所以f(x)的最小正周期为4,
即T=$\frac{2π}{ω}$=4,解得ω=$\frac{π}{2}$;
所以f(x)=2sin($\frac{π}{2}$x+$\frac{π}{3}$),
所以f(1)+f(2)+f(3)+…+f(9)
=2sin($\frac{π}{2}$+$\frac{π}{3}$)+2sin(π+$\frac{π}{3}$)+2sin($\frac{3π}{2}$+$\frac{π}{3}$)+…+2sin($\frac{9π}{2}$+$\frac{π}{3}$)
=2cos$\frac{π}{3}$
=1.
故选:A.
点评 本题考查了三角函数的化简与求值问题,是基础题目.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
19.已知集合A={x∈Z|(x+2)(x-1)<0},B={-2,-1},那么A∪B等于( )
| A. | {-2,-1,0,1} | B. | {-2,-1,0} | C. | {-2,-1} | D. | {-1} |
14.如果函数y=sin(x+ϕ)的图象经过点$(\frac{π}{3},0)$,那么ϕ可以是( )
| A. | 0 | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
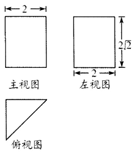 《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为16π.
《九章算术》中将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的外接球的表面积为16π.