题目内容
9.已知方程3x+x=5的根在区间[k,k+1)(k∈Z),则k的值为1.分析 方程3x+x=5的解转化为函数f(x)=3x+x-5的零点问题,把区间端点函数值代入验证即可.
解答 解:令f(x)=3x+x-5,
由y=3x和y=x-5均为增函数,
故f(x)=3x+x-5在R上为增函数,
故f(x)=3x+x-5至多有一个零点,
∵f(1)=3+1-5<0
f(2)=9+2-5>0
∴f(x)=3x+x-5在区间[1,2]有一个零点,
即方程方程3x+x=5的解所在区间为[1,2],
故k=1,
故答案为:1
点评 考查方程的根和函数零点之间的关系,即函数零点的判定定理,体现了转化的思想方法,属基础题.

练习册系列答案
相关题目
19.已知函数f(x)的图象如图所示,则该函数的定义域、值域分别是( )
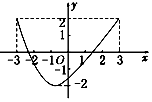

| A. | (-3,3),(-2,2) | B. | [-2,2],[-3,3] | C. | [-3,3],[-2,2] | D. | (-2,2),(-3,3) |
4.如果函数f(x)=sinωx+$\sqrt{3}$cosωx的两个相邻零点间的距离为2,那么f(1)+f(2)+f(3)+…+f(9)的值为( )
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
19.已知f(x)是定义在R上的偶函数,且f(x)在[0,+∞)是减函数,若f(lgx)>f(1),则x的取值范围是( )
| A. | $(\frac{1}{10},10)$ | B. | (0,10) | C. | (10,+∞) | D. | $(0,\frac{1}{10})∪(10,+∞)$ |
 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,且过点($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,且过点($\frac{\sqrt{3}}{2}$,$\frac{1}{4}$).