题目内容
15.已知△ABC的顶点A(5,1),AB边上的中线CM所在的直线方程为2x-y-5=0,AC边上的高BH所在的直线方程为x-2y-5=0.求(Ⅰ)AC所在的直线方程;
(Ⅱ)点B的坐标.
分析 (Ⅰ)设AC所在的直线方程为2x+y+t=0,代入A(5,1),即可AC所在的直线方程;
(Ⅱ)设B(x0,y0),则AB的中点为$(\frac{{{x_0}+5}}{2},\frac{{{y_0}+1}}{2})$.联立方程组$\left\{\begin{array}{l}{x_0}-2{y_0}-5=0\\ 2×\frac{{{x_0}+5}}{2}-\frac{{{y_0}+1}}{2}-5=0.\end{array}\right.$,即可求出点B的坐标.
解答 解:(Ⅰ)因为AC⊥BH,所以设AC所在的直线方程为2x+y+t=0.
把A(5,1)代入直线方程为2x+y+t=0,解得t=-11.
所以AC所在的直线方程为2x+y-11=0. …(5分)
(Ⅱ)设B(x0,y0),则AB的中点为$(\frac{{{x_0}+5}}{2},\frac{{{y_0}+1}}{2})$.
联立方程组$\left\{\begin{array}{l}{x_0}-2{y_0}-5=0\\ 2×\frac{{{x_0}+5}}{2}-\frac{{{y_0}+1}}{2}-5=0.\end{array}\right.$化简得$\left\{\begin{array}{l}{x_0}-2{y_0}-5=0\\ 2{x_0}-{y_0}-1=0.\end{array}\right.$
解得$\left\{\begin{array}{l}{x_0}=-1\\{y_0}=-3.\end{array}\right.$即B(-1,-3). …(9分)
点评 本题考查直线方程,考查直线与直线的位置关系,考查学生的计算能力,属于中档题.

 53随堂测系列答案
53随堂测系列答案| A. | 若α⊥β,则m⊥n | B. | 若α∥β,则m∥n | C. | 若m⊥n,则α⊥β | D. | 若n⊥α,则α⊥β |
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $-\frac{3}{4}$ |
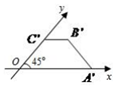 一直角梯形的直观图是一个如图所示的梯形,且OA′=2,B′C′=OC′=1,则该直角梯形的面积为( )
一直角梯形的直观图是一个如图所示的梯形,且OA′=2,B′C′=OC′=1,则该直角梯形的面积为( )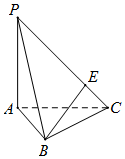 如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.
如图,在三棱锥P-ABC中,PA⊥平面ABC,AB=BC,PA=AC,E为PC上的动点,当 BE⊥PC时,$\frac{CE}{PC}$的值为$\frac{1}{4}$.