题目内容
11.已知函数f(x)是定义在R上的可导函数,其导函数为f′(x),则命题P:“?x1,x2∈R,且x1≠x2,|$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$|<2017”是命题Q:“?x∈R,|f′(x)|<2017”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 由Q⇒P,反之不成立.即可判断出结论.
解答 解:命题Q:“?x∈R,|f′(x)|<2017”⇒?x1,x2∈R,且x1≠x2,|$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$|<2017;
反之不一定成立,由?x1,x2∈R,且x1≠x2,|$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$|<2017可能得到:?x∈R,|f′(x)|≤2017.
∴命题P是Q的必要不充分条件.
故选:B.
点评 本题考查了导数的性质及其几何意义、割线的斜率,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.执行如图所示的程序框图,则输出的S值为( )
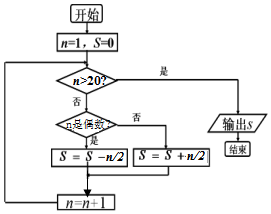

| A. | 10 | B. | -10 | C. | 5 | D. | -5 |
6.若($\frac{1}{x}$+2x)6展开式的常数项为( )
| A. | 120 | B. | 160 | C. | 200 | D. | 240 |
20.α是一个平面,m,n是两条直线,A是一个点,若m?α,n?α,且A∈m,A∈α,则m,n的位置关系不可能是( )
| A. | 垂直 | B. | 相交 | C. | 异面 | D. | 平行 |
 在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.
在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.