题目内容
12.已知曲线C:$\left\{\begin{array}{l}x=\frac{{\sqrt{2}}}{2}t\\ y=a+\frac{{\sqrt{2}}}{2}t\end{array}$(t为参数),A(-1,0),B(1,0),若曲线C上存在点P满足$\overrightarrow{AP}$•$\overrightarrow{BP}$=0,则实数a的取值范围为( )| A. | $[{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}}]$ | B. | [-1,1] | C. | $[{-\sqrt{2},\sqrt{2}}]$ | D. | [-2,2] |
分析 求出P的轨迹方程,直线的普通方程,利用直线与圆有交点,即可得出结论.
解答 解:∵A(-1,0),B(1,0),若曲线C上存在点P满足$\overrightarrow{AP}$•$\overrightarrow{BP}$=0,
∴P的轨迹方程是x2+y2=1.
曲线C:$\left\{\begin{array}{l}x=\frac{{\sqrt{2}}}{2}t\\ y=a+\frac{{\sqrt{2}}}{2}t\end{array}$(t为参数),普通方程为x-y+a=0,
由题意,圆心到直线的距离d=$\frac{|a|}{\sqrt{2}}$≤1,∴$-\sqrt{2}≤a≤\sqrt{2}$,
故选C.
点评 本题考查轨迹方程,考查参数方程与普通方程的转化,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.执行如图所示的程序框图,则输出的S值为( )
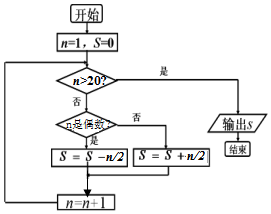

| A. | 10 | B. | -10 | C. | 5 | D. | -5 |
20.α是一个平面,m,n是两条直线,A是一个点,若m?α,n?α,且A∈m,A∈α,则m,n的位置关系不可能是( )
| A. | 垂直 | B. | 相交 | C. | 异面 | D. | 平行 |
7.一个几何体的三视图如图所示,则该几何体的体积为( )


| A. | 4$\sqrt{3}$ | B. | 4$\sqrt{2}$ | C. | 4 | D. | $\frac{{4\sqrt{3}}}{3}$ |




 在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.
在四棱锥S-ABCD中,底面ABCD为平行四边形,∠DBA=60°,∠SAD=30°,AD=SD=2$\sqrt{3}$,BA=BS=4.