题目内容
8.定义在R上的函数f(x)满足f(x)=$\left\{\begin{array}{l}{log_2}(8-x),x≤0\\ f(x-1),x>0\end{array}$则f(3)=( )| A. | 3 | B. | 2 | C. | log29 | D. | log27 |
分析 由已知中f(x)=$\left\{\begin{array}{l}{log_2}(8-x),x≤0\\ f(x-1),x>0\end{array}$,将x=3代入可得答案.
解答 解:∵f(x)=$\left\{\begin{array}{l}{log_2}(8-x),x≤0\\ f(x-1),x>0\end{array}$,
∴f(3)=f(2)=f(1)=f(0)=log28=3,
故选:A
点评 本题考查的知识点是函数求值,分段函数的应用,难度不大,属于基础题.

练习册系列答案
相关题目
18.设i是虚数单位,则复数(2+i)(1-i)的虚部为( )
| A. | i | B. | -1 | C. | 3 | D. | -i |
13.某厂在生产某产品的过程中,产量x(吨)与生产能耗y(吨)的对应数据如表所示.根据最小二乘法求得回归直线方程为$\widehat{y}$=0.7x+a.当产量为80吨时,预计需要生产能耗为59.5吨.
| x | 30 | 40 | 50 | 60 |
| y | 25 | 30 | 40 | 45 |
20.α是一个平面,m,n是两条直线,A是一个点,若m?α,n?α,且A∈m,A∈α,则m,n的位置关系不可能是( )
| A. | 垂直 | B. | 相交 | C. | 异面 | D. | 平行 |
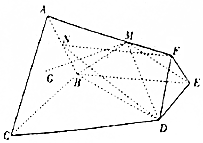 如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.
如图在棱台ABC-FED中,△DEF与△ABC分别是边长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,点G为△ABC的重心,N为AB的中点,点M是侧棱AF上的点且$\frac{AM}{AF}$=λ.