题目内容
设数列{an}(n∈N)满足a0=0,a1=2,且对一切n∈N,有an+2=2an+1-an+2.
(1)求a2,a3的值;
(2)证明:数列{an-an-1}为等差数列;
(3)数列{an}的通项公式;
(4)设Tn=
+
+
+…+
,求证:Tn<
.
(1)求a2,a3的值;
(2)证明:数列{an-an-1}为等差数列;
(3)数列{an}的通项公式;
(4)设Tn=
| 1 |
| 3a1 |
| 1 |
| 4a2 |
| 1 |
| 5a3 |
| 1 |
| (n+2)an |
| 1 |
| 4 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用递推式即可得出;
(2)an+2=2an+1-an+2,可得(an+2-an+1)-(an+1-an)=2,即可证明;
(3)利用等差数列的通项公式与“累加求和”即可得出;
(4)由(2)可知:
=
=
[
-
],利用“裂项求和”即可得出.
(2)an+2=2an+1-an+2,可得(an+2-an+1)-(an+1-an)=2,即可证明;
(3)利用等差数列的通项公式与“累加求和”即可得出;
(4)由(2)可知:
| 1 |
| (n+2)an |
| 1 |
| (n+2)n(n+1) |
| 1 |
| 2 |
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
解答:
(1)解:∵a0=0,a1=2,且对一切n∈N,有an+2=2an+1-an+2.
∴a2=2a1-a0+2=2×2-0+2=6,
a3=2a2-a1+2=2×6-2+2=12.
(2)证明:∵an+2=2an+1-an+2,
∴an+2-an+1=an+1-an+2,
化为(an+2-an+1)-(an+1-an)=2,
∴数列{an-an-1}为等差数列,且首项 a1-a0=2-0=2,公差为2.
(3)解:由(2)可得an-an-1=a1-a0+2(n-1)=2+2(n-1)═2n.
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+4+6+…++2n=
=n(n+1).
(4)证明:由(2)可知:
=
=
[
-
],
∴Tn=
+
+
+…+
=
[(
-
)+(
-
)+…+(
-
)]
=
[
-
]=
-
<
.
∴Tn<
.
∴a2=2a1-a0+2=2×2-0+2=6,
a3=2a2-a1+2=2×6-2+2=12.
(2)证明:∵an+2=2an+1-an+2,
∴an+2-an+1=an+1-an+2,
化为(an+2-an+1)-(an+1-an)=2,
∴数列{an-an-1}为等差数列,且首项 a1-a0=2-0=2,公差为2.
(3)解:由(2)可得an-an-1=a1-a0+2(n-1)=2+2(n-1)═2n.
∴an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2+4+6+…++2n=
| n(2+2n) |
| 2 |
(4)证明:由(2)可知:
| 1 |
| (n+2)an |
| 1 |
| (n+2)n(n+1) |
| 1 |
| 2 |
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
∴Tn=
| 1 |
| 3a1 |
| 1 |
| 4a2 |
| 1 |
| 5a3 |
| 1 |
| (n+2)an |
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
=
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| (n+1)(n+2) |
| 1 |
| 4 |
| 1 |
| 2(n+1)(n+2) |
| 1 |
| 4 |
∴Tn<
| 1 |
| 4 |
点评:本题考查了等差数列的通项公式及其前n项和公式、“累加求和”、“裂项求和”,考查了变形能力,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
下列命题中,真命题是( )
| A、“a≤b”是“a+c≤b+c”的充分不必要条件 | ||||||||
| B、“已知x,y∈R,若x+y≠6,则x≠2或y≠4”是真命题 | ||||||||
| C、二进制数1010(2) 可表示为三进制数110(3) | ||||||||
D、“平面向量
|
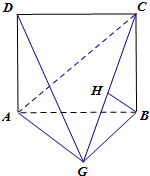 已知四棱锥G-ABCD,四边形ABCD是长为2a的正方形,DA⊥平面ABG,且GA=GB,BH⊥平面CAG,垂足为H,且H在直线CG上.
已知四棱锥G-ABCD,四边形ABCD是长为2a的正方形,DA⊥平面ABG,且GA=GB,BH⊥平面CAG,垂足为H,且H在直线CG上.