题目内容
已知函数y=x2和y=x3.
(1)它们的奇偶性是怎样的?
(2)它们的图象各有怎样的对称性?
(3)它们在(0,+∞)上各有怎样的单调性?在(-∞,0)上呢?
(1)它们的奇偶性是怎样的?
(2)它们的图象各有怎样的对称性?
(3)它们在(0,+∞)上各有怎样的单调性?在(-∞,0)上呢?
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:计算题,函数的性质及应用
分析:运用奇偶性的定义,即可得到(1),再由奇偶函数图象的特点,即可得到(2),再由它们的图象即可得到函数的单调性.
解答:
解:(1)函数y=x2,由f(-x)=f(x)可得为偶函数,
函数y=x3,由f(-x)=-f(x),可知为奇函数;
(2)函数y=x2,的图象关于y轴对称,函数y=x3,的图象关于原点对称;
(3)函数y=x2在(0,+∞)上递增,在(-∞,0)上递减;
函数y=x3在(0,+∞)上递增,在(-∞,0)上递增.
函数y=x3,由f(-x)=-f(x),可知为奇函数;
(2)函数y=x2,的图象关于y轴对称,函数y=x3,的图象关于原点对称;
(3)函数y=x2在(0,+∞)上递增,在(-∞,0)上递减;
函数y=x3在(0,+∞)上递增,在(-∞,0)上递增.
点评:本题考查函数的奇偶性和单调性的判断,考查奇偶函数的图象特点,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若圆(x-a)2+(y-b)2=c2和圆(x-b)2+(y-a)2=c2相切,则( )
| A、(a-b)2=c2 |
| B、(a-b)2=2c2 |
| C、(a+b)2=c2 |
| D、(a+b)2=2c2 |
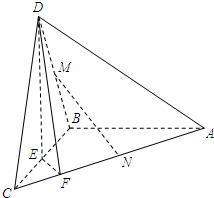 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC,E为BC的中点,F在棱AC上,且AF=3FC,