Question

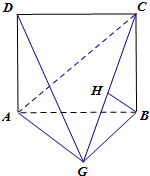已知四棱锥G-ABCD，四边形ABCD是长为2a的正方形，DA⊥平面ABG，且GA=GB，BH⊥平面CAG，垂足为H，且H在直线CG上．
（1）求证：平面AGD⊥平面BGC；
（2）求三棱锥D-ACG的体积；
（3）求三棱锥D-ACG的内切球半径．

Answer 1

考点：平面与平面垂直的判定,球的体积和表面积

专题：综合题,空间位置关系与距离

分析：（1）过点B作平面AGC的垂线，垂足H在CG上，由ABCD是正方形，面ABCD⊥面ABG，由面面垂直的性质可得BC⊥面ABG，则BC⊥AG，又由BH⊥面AGC得BH⊥AG，由线面垂直的判定定理可得AG⊥面AGD后，可由面面垂直的判定定理得到面AGD⊥面BGC 
（2）△ABG中AG⊥BG且AG=BG，取AB中点E，连接GE，则GE⊥AB，利用等积法可得三棱锥D-ACG的体积；
（3）利用等体积求三棱锥D-ACG的内切球半径．

解答： （1）证明：过点B作平面AGC的垂线，垂足H在CG上，则
∵ABCD是正方形，
∴BC⊥AB，
∵面ABCD⊥面ABG，
∴BC⊥面ABG，
∵AG?面ABG，
∴BC⊥AG，
又BH⊥面AGC，
∴BH⊥AG，
又∵BC∩BH=B，
∴AG⊥面AGD，
∴面AGD⊥面BGC；
（2）解：由（1）知AG⊥面BGC，
∴AG⊥BG，
又AG=BG，
∴△ABG是等腰Rt△，取AB中点E，连接GE，则GE⊥AB
∴GE⊥面ABCD
∴V_D-ACG=V_G-ACD=

1

3

GE•S_△ACD=

1

3

•

1

2

•2a•

1

2

（2a）²=

2

3

a3；
（3）解：记三棱锥内切球的半径为r，VG-ADC=

1

3

(S△DCG+S△AGC+S△DAG+S△ADC)•r=

2

3

a3，
△DCG中，DG=GC=

6

a，DC=2a，S_△DOG=

5

a2，
△ACG中，AC=2

2

a，GC=

6

a，AG=

2

a，S_△ACG=

3

a2，
△DAG中，DA=2a，AG=

2

a，S_△DAG=

2

a2，
△ADC中，S_△DAC=2a²
由VG-ADC=

1

3

(S△DCG+S△AGC+S△DAG+S△ADC)•r=

2

3

a3，
可得r=

2

5 + 3 + 2 +2

a．

点评：本题考查的知识点是平面与平面垂直的判定，三棱锥的体积，其中（1）要熟练掌握空间中线线垂直，线面垂直及面面垂直之间的相互转化，属于中档题．