题目内容
椭圆
+
=1的焦点坐标是 ,离心率是 .
| x2 |
| 16 |
| y2 |
| 25 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:先求出a,b,c的值,从而求出焦点坐标和离心率的值.
解答:
解:∵a2=25,b2=16,
∴c2=25-16=9,
∴c=3,
∴焦点坐标是(0,3),(0,-3);
e=
=
,
故答案为:(0,3),(0,-3),
.
∴c2=25-16=9,
∴c=3,
∴焦点坐标是(0,3),(0,-3);
e=
| c |
| a |
| 3 |
| 5 |
故答案为:(0,3),(0,-3),
| 3 |
| 5 |
点评:本题考查了椭圆的简单性质,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设方程x2+y2+2ax+2by+a2=0表示圆,则下列点中,必位于圆外的点是( )
| A、(0,0) |
| B、(1,0) |
| C、(a,b) |
| D、(a,-b) |
若方程
-
=1表示双曲线,则实数k的取值范围是( )
| x2 |
| 3-k |
| y2 |
| k-1 |
| A、k<1 | B、1<k<3 |
| C、k>3 | D、k<1或k>3 |
平行于直线2x-y+1=0且与圆x2+y2=5相切的直线方程是( )
| A、2x-y+5=0 |
| B、2x-y-5=0 |
| C、2x-y±5=0 |
| D、2x+y±5=0 |
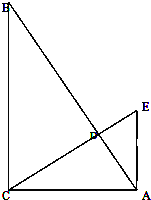 △ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.
△ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.