题目内容
某中学从17~18岁的学生中抽样50人进行身高、体重调查,结果如下:
已知从这50名学生中任取1人体重超常的概率是
.
(1)求表中x与y的值;
(2)从体重和身高都偏高或超常的学生中任取2名,求其中有1名学生体重和身高都超常的概率.
| 体重 身高 |
偏低 | 中等 | 偏高 | 超常 |
| 偏低 | 1 | 1 | 2 | 1 |
| 中等 | 2 | 10 | 7 | y |
| 偏高 | 6 | x | 1 | 1 |
| 超常 | 1 | 4 | 2 | 1 |
| 1 |
| 10 |
(1)求表中x与y的值;
(2)从体重和身高都偏高或超常的学生中任取2名,求其中有1名学生体重和身高都超常的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)利用体重超常的概率是
.求出体重超常的学生数,可求得x,再求y;
(2)求出体重和身高都偏高或超常的学生数,分别求出从中任选2人的选法种数与其中有1名学生体重和身高都超常的选法种数,代入概率公式计算可得.
| 1 |
| 10 |
(2)求出体重和身高都偏高或超常的学生数,分别求出从中任选2人的选法种数与其中有1名学生体重和身高都超常的选法种数,代入概率公式计算可得.
解答:
解:(1)∵体重超常的概率是
.∴体重超常的学生数为
×50=5,
∴y=2,∵样本容量为50,∴x=8.
(2)由列联表知:体重和身高都偏高或超常的学生共有5人,
从中任选2人有
=10种选法,
其中有1名学生体重和身高都超常的有4种选法,
∴有1名学生体重和身高都超常的概率为
.
| 1 |
| 10 |
| 1 |
| 10 |
∴y=2,∵样本容量为50,∴x=8.
(2)由列联表知:体重和身高都偏高或超常的学生共有5人,
从中任选2人有
| C | 2 5 |
其中有1名学生体重和身高都超常的有4种选法,
∴有1名学生体重和身高都超常的概率为
| 2 |
| 5 |
点评:本题考查利用列联表求概率及古典概型的概率计算,关键是读懂列联表.

练习册系列答案
相关题目
设数列{an}的前n项和为Sn,令Tn=
,称Tn为数列a1,a2,…,an的“理想数”,已知数列a1,a2,…,a502的“理想数”为2012,那么数列3,a1,a2,…,a502的“理想数”为( )
| S1+S2+…+Sn |
| n |
| A、2011 | B、2012 |
| C、2013 | D、2014 |
在区间[0,1]上任取两个数a,b,则函数f(x)=x2+ax+b2无零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
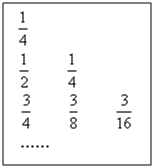 如图给出一个“直角三角形数阵”:满足每一列成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N+),则a86=( )
如图给出一个“直角三角形数阵”:满足每一列成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N+),则a86=( )A、
| ||
B、
| ||
C、
| ||
D、
|
不等式
≥3的解集为 ( )
| 2x+1 |
| x |
| A、[-1,0) |
| B、[-1,+∞) |
| C、(0,1] |
| D、(-∞,-1]∪(0,+∞) |
三个数0.993.3,log3π,log20.8的大小关系为( )
| A、log3π<0.993.3<log20.8 |
| B、log20.8<log3π<0.993.3 |
| C、log20.8<0.993.3<log3π |
| D、0.993.3<log20.8 l<log3π |