题目内容
若直线x+
y+1=0与圆x2+y2+mx=0相切,则实数m的值是 .
| 3 |
考点:圆的切线方程,圆的一般方程
专题:计算题,直线与圆
分析:将圆化成标准方程,得圆心为C(-
,0)、半径r=
.由直线x+
y+1=0与圆相切,可得圆心C到直线的距离等于半径,根据点到直线的距离公式建立关于m的等式,解之即可得到实数m的值.
| m |
| 2 |
| |m| |
| 2 |
| 3 |
解答:
解:圆x2+y2+mx=0化成标准方程,得(x+
)2+y2=
m2,
∴圆心为C(-
,0),半径r=
.
∵直线x+
y+1=0与圆x2+y2+mx=0相切,
∴圆心C到直线的距离等于半径,
即
=
,解之得m=
或-2.
故答案为:
或-2
| m |
| 2 |
| 1 |
| 4 |
∴圆心为C(-
| m |
| 2 |
| |m| |
| 2 |
∵直线x+
| 3 |
∴圆心C到直线的距离等于半径,
即
|-
| ||||
|
| |m| |
| 2 |
| 2 |
| 3 |
故答案为:
| 2 |
| 3 |
点评:本题给出直线与圆相切,求参数m之值.着重考查了圆的标准方程、点到直线的距离公式和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
在区间[0,1]上任取两个数a,b,则函数f(x)=x2+ax+b2无零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
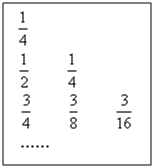 如图给出一个“直角三角形数阵”:满足每一列成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为
如图给出一个“直角三角形数阵”:满足每一列成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为