题目内容
已知直线L：x+y-9=0和圆M：2x2+2y2-8x-8y-1=0，点A在直线L上，B，C为圆M上的两点，在△ABC中，∠BAC=45°，AB过圆心M，则点A的横坐标取值范围为（ ）
| A、[0，3] |
| B、[3，6] |
| C、（0，3] |
| D、（3，6） |
考点：直线与圆的位置关系
专题：直线与圆
分析：圆的方程化为标准方程，设A（a，9-a），①当a≠2时，把∠BAC看作AB到AC的角，又点C在圆M，由圆心到AC的距离小于等于圆的半径，求出a的范围；②当a=2时，则A（2，7）与直线x=2成45°角的直线有x-y+5=0，或x+y-9=0，判断这样点C不在圆M上不成立．
解答：
解：圆M：2x2+2y2-8x-8y-1=0方程可化为（x-2）2+（y-2）2=（
）2，
设A点的横坐标为a，则纵坐标为9-a；
①当a≠2时，kAB=
，设AC的斜率为k，把∠BAC看作AB到AC的角，则可得k=
，
直线AC的方程为y-（9-a）=
（x-a）
即5x-（2a-9）y-2a2+22a-81=0，
又点C在圆M上，所以只需圆心到AC的距离小于等于圆的半径，即
≤
，
化简得a2-9a+18≤0，解得3≤a≤6；
②当a=2时，则A（2，7）与直线x=2成45°角的直线为x-y+5=0，或x+y-9=0
M到x-y+5=0的距离d=
=
＞
，这样点C不在圆M上，
同理x+y-9=0，显然也不满足条件，
综上：A点的横坐标范围为[3，6]．
故选B．
| ||
| 2 |
设A点的横坐标为a，则纵坐标为9-a；
①当a≠2时，kAB=
| 7-a |
| a-2 |
| 5 |
| 2a-9 |
直线AC的方程为y-（9-a）=
| 5 |
| 2a-9 |
即5x-（2a-9）y-2a2+22a-81=0，
又点C在圆M上，所以只需圆心到AC的距离小于等于圆的半径，即
| |10-2(2a-9)-2a2+22a-81| | ||
|
| ||
| 2 |
化简得a2-9a+18≤0，解得3≤a≤6；
②当a=2时，则A（2，7）与直线x=2成45°角的直线为x-y+5=0，或x+y-9=0
M到x-y+5=0的距离d=
| |2-2+5| | ||
|
5
| ||
| 2 |
| ||
| 2 |
同理x+y-9=0，显然也不满足条件，
综上：A点的横坐标范围为[3，6]．
故选B．
点评：本题主要考查直线与圆的位置关系及方程的应用，考查直线中的到角公式，点到直线的距离，考查分类讨论的数学思想，属于中档题．
练习册系列答案
相关题目
若集合A={x∈R|y=lg（2-x）}，B={y∈R|y=2x-1，x∈A}，则∁R（A∩B）=（ ）
| A、R |
| B、（-∞，0]∪[2，+∞） |
| C、[2，+∞） |
| D、（-∞，0] |
如图，已知椭圆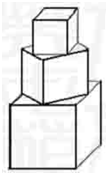
有一塔形几何体由若干个正方体构成，构成方式如图所示，上层正方体下底面的四个顶点是下层正方体上底面各边中点，已知最底层正方体的棱长为2，且该塔形的表面积（含C最底层正方体的底面面积）超过39，则该塔形中正方体的个数至少是