题目内容
设[x]表示不大于x的最大整数,则函数f(x)=lg2x-[lgx]-2的零点个数是( )
| A、4 | B、3 | C、2 | D、1 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:函数f(x)=lg2x-[lgx]-2的零点,即方程lg2x-[lgx]-2=0的根,先进行换元,令lgx=t,则得t2-2=[t],作y=t2-2与y=[t]的图象可得解的个数.
解答:
解:函数f(x)=lg2x-[lgx]-2的零点,
即方程lg2x-[lgx]-2=0的根,
令lgx=t,则得t2-2=[t].
作y=t2-2与y=[t]的图象,
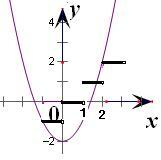
知t=-1,t=2,及1<t<2内有一解.
当1<t<2时,[t]=1,t=
.
故得:x=
,x=100,x=10
,即共有3个实根,
故选:B
即方程lg2x-[lgx]-2=0的根,
令lgx=t,则得t2-2=[t].
作y=t2-2与y=[t]的图象,

知t=-1,t=2,及1<t<2内有一解.
当1<t<2时,[t]=1,t=
| 3 |
故得:x=
| 1 |
| 10 |
| 3 |
故选:B
点评:本题主要考查了根的个数的判定,以及图象法的运用,同时考查了分析问题的能力,属于中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
关于x的不等式x2-ax+a>0(a∈R)在R上恒成立的充分不必要条件是( )
| A、a<0或a>4 |
| B、0<a<2 |
| C、0<a<4 |
| D、0<a<8 |
已知向量
,
满足|
|=1,|
|=2,
与
的夹角为60°,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
| C、1 | ||
| D、3 |
利用回归分析的方法研究两个具有线性相关关系的变量时,下列说法中表述错误的是( )
| A、相关系数r满足|r|≤1,而且|r|越接近1,变量间的相关程度越大,|r|越接近0,变量间的相关程度越小 |
| B、可以用R2来刻画回归效果,对于已获取的样本数据,R2越小,模型的拟合效果越好 |
| C、如果残差点比较均匀地落在含有x轴的水平的带状区域内,那么选用的模型比较合适;这样的带状区域越窄,回归方程的预报精度越高 |
| D、不能期望回归方程得到的预报值就是预报变量的精确值 |
已知△ABC是边长为4的等边三角形,点D、E分别满足
=-
、
=
,则
•
=( )
| DC |
| AC |
| BE |
| EC |
| AB |
| DE |
| A、8 | B、4 | C、-8 | D、-4 |
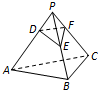 如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足DE=EF=3,DF=2的△DEF个数是( )
如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足DE=EF=3,DF=2的△DEF个数是( )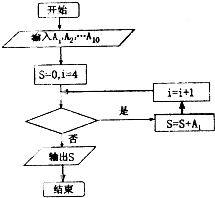 如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )
如表是我市抽查部分高中学生的身高统计表,从左到右的各组表示的学生人数依次记为A1,A2,…,A10(如A2表示身高[150,155)内的人数),如图是统计表中身高在一定范围内的学生人数的程序框图,如果要统计身高在160-180cm(含160cm不含180cm)的学生人数,那么空白的判断框内应填写的条件是( )