题目内容
8.过P(-4,1)的直线?与抛物线y2=4x仅有一个公共点,则这样的直线?有( )条.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设出直线方程代入抛物线方程整理可得k2x2+(4k2+2k-4)x+4k2+4k+1=0(*)直线与抛物线只有一个公共点?(*)只有一个根.
解答 解:由题意可设直线方程为:y=k(x+4)+1,
代入抛物线方程整理可得k2x2+(8k2+2k-4)x+16k2+8k+1=0(*)
直线与抛物线只有一个公共点等价于(*)只有一个根
①k=0时,y=1符合题意;
②k≠0时,△=(8k2+2k-4)2-4k2(16k2+8k+1)=0,整理,得2k2-k+1=0,
解得k=1 或k=$\frac{1}{2}$.
满足题意的直线有3条.
故选:C.
点评 本题主要考查了由直线与抛物线的位置关系的求解参数的取值范围,一般的思路是把位置关系转化为方程解的问题,体现了转化的思想.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
16.已知数列{an}(n=1,2,3,…,2014),圆C1:x2+y2-4x-4y=0,圆C2:x2+y2-2anx-2a2015-ny=0,若圆C2平分圆C1的周长,则{an}的所有项的和为( )
| A. | 4028 | B. | 4026 | C. | 2014 | D. | 2013 |
3.已知函数f(x)=log2x,若在[1,8]上任取一个实数x0,则不等式1≤f(x0)≤2成立的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{7}$ | D. | $\frac{2}{5}$ |
17.已知函数f(x)=$\frac{a•{3}^{x}-2}{{3}^{x}+1}$为奇函数,则函数g(x)=x+$\frac{a}{x}$(x>0)的单调递增区间为( )
| A. | (0,$\sqrt{2}$) | B. | (0,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
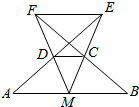 已知:如图,AB∥CD,M是AB的中点,MC的延长线与AD的延长线交于点E,MD的延长线与BC的延长线交于点F.求证:EF∥AB.
已知:如图,AB∥CD,M是AB的中点,MC的延长线与AD的延长线交于点E,MD的延长线与BC的延长线交于点F.求证:EF∥AB.