Question

13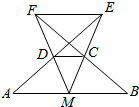．已知：如图，AB∥CD，M是AB的中点，MC的延长线与AD的延长线交于点E，MD的延长线与BC的延长线交于点F．求证：EF∥AB．

Answer 1

分析 AB∥CD，可得△MFB∽△DFC，△MEA∽△CED，证明△CMD∽△EMF，可得∠MCD=∠MEF，即可证明结论．

解答 证明：∵AB∥CD，∴△MFB∽△DFC，△MEA∽△CED，
∴$\frac{FM}{FD}$=$\frac{CD}{BM}$，$\frac{EC}{EM}$=$\frac{CD}{AM}$，
又BM=AM．
∴$\frac{FM}{FD}$=$\frac{EC}{EM}$，
又∠EMF=∠CMD，∴△CMD∽△EMF，
∴∠MCD=∠MEF，
∴CD∥EF，
∴EF∥AB．

点评 本题考查三角形相似的判定与性质，考查学生分析解决问题的能力，属于中档题．