题目内容
18.设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+x,x<0}\\{-{x}^{2},x≥0}\end{array}\right.$,则方程f(f (x) )=2的解是$\sqrt{2}$.分析 利用分段函数与复合函数知f2(x)+f(x)=2,从而解得f(x)=-2,从而可得x2+x=-2或-x2=-2,从而解得.
解答 解:∵f(f (x) )=2,
∴f2(x)+f(x)=2,
解得,f(x)=1或f(x)=-2,
故x2+x=-2或-x2=-2,
故x=-$\sqrt{2}$(舍去)或x=$\sqrt{2}$;
故答案为:$\sqrt{2}$.
点评 本题考查了分段函数的应用及分类讨论的思想应用.

练习册系列答案
相关题目
9.若实数x,y满足$\left\{\begin{array}{l}{2x+y≤8}\\{x+y≥a}\\{x≥0}\end{array}\right.$,且z=60x+20y的最大值为200,则a等于( )
| A. | 4 | B. | 6 | C. | 3 | D. | 9 |
13.x2-ax+b>0的解集为{x|x<2或x>3},则a+b的值是( )
| A. | 1 | B. | -1 | C. | 11 | D. | 12 |
8.过P(-4,1)的直线?与抛物线y2=4x仅有一个公共点,则这样的直线?有( )条.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
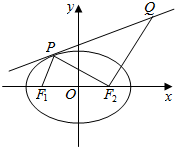 已知F1,F2是椭圆$Γ:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点,椭圆Γ的离心率$e=\frac{{\sqrt{2}}}{2}$,P(x0,y0)是Γ上异于左右顶点的任意一点,且△PF1F2的面积的最大值为1.
已知F1,F2是椭圆$Γ:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左右焦点,椭圆Γ的离心率$e=\frac{{\sqrt{2}}}{2}$,P(x0,y0)是Γ上异于左右顶点的任意一点,且△PF1F2的面积的最大值为1.