题目内容
3．已知函数f（x）=log2x，若在[1，8]上任取一个实数x0，则不等式1≤f（x0）≤2成立的概率是（ ）| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{7}$ | D． | $\frac{2}{5}$ |
分析 根据对数不等式的解法求出不等式的等价条件，根据几何概型的概率公式进行计算即可．
解答 解：∵由1≤f（x0）≤2得1≤log2x0≤2，∴2≤x0≤4，
则不等式1≤f（x0）≤2成立的概率是P=$\frac{4-2}{8-1}$=$\frac{2}{7}$，
故选：C
点评 本题主要考查几何概型的概率的计算，求出不等式的等价条件是解决本题的关键．
练习册系列答案
相关题目
13．x2-ax+b＞0的解集为{x|x＜2或x＞3}，则a+b的值是（ ）
| A． | 1 | B． | -1 | C． | 11 | D． | 12 |
11．已知函数$f（x）=\left\{{\begin{array}{l}{\frac{1}{2}x+1，x≤2}\\{lnx，x＞2}\end{array}}\right.$，方程f（x）-ax=0恰有3个不同实根，则实数a的取值范围是（ ）
| A． | $（\frac{ln2}{2}，\frac{1}{e}）$ | B． | $（0，\frac{1}{2}）$ | C． | $（0，\frac{1}{e}）$ | D． | $（\frac{1}{e}，\frac{1}{2}）$ |
18．已知函数$f（x）=a-\frac{4}{{{2^x}+1}}（{a∈R}）$是定义在（-∞，+∞）上的奇函数．
（1）求a的值，并写出函数f（x）的解析式；
（2）求证：函数f（x）在上是增函数．
（1）求a的值，并写出函数f（x）的解析式；
（2）求证：函数f（x）在上是增函数．
8．过P（-4，1）的直线?与抛物线y2=4x仅有一个公共点，则这样的直线?有（ ）条．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
15．下列选项中是函数f（x）=sinx-$\sqrt{3}$cosx的零点的是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{2π}{3}$ | C． | $\frac{7π}{6}$ | D． | $\frac{4π}{3}$ |
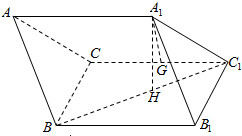在三棱柱ABC-A1B1C1中，面BB1C1C是边长为2的正方形，点A1在平面BB1C1C上的射影H是BC1的中点，且A1H=$\sqrt{3}$，G是CC1的中点．