Question

16．已知数列{a_n}（n=1，2，3，…，2014），圆C₁：x²+y²-4x-4y=0，圆C₂：x²+y²-2a_nx-2a_2015-ny=0，若圆C₂平分圆C₁的周长，则{a_n}的所有项的和为（　　）

• A． 4028
• B． 4026
• C． 2014
• D． 2013

Answer 1

分析 由题意知C₁（2，2），C₂（a_n，a_2015-n），且易知圆C₁与圆C₂相交于原点，且交点弦是圆C₁的直径，从而可得a_n+a_2015-n=4，从而解得．

解答 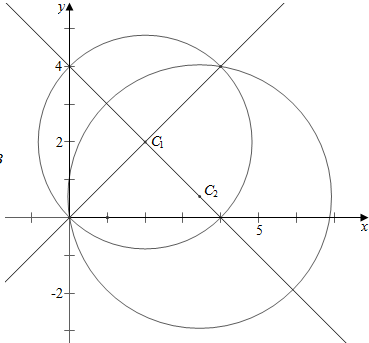解：∵圆C₁：x²+y²-4x-4y=0，圆C₂：x²+y²-2a_nx-2a_2015-ny=0，
∴C₁（2，2），C₂（a_n，a_2015-n）；
且易知圆C₁与圆C₂相交于原点，
又∵圆C₂平分圆C₁的周长，
∴交点弦是圆C₁的直径，
∴作圆C₁与圆C₂的图象如右图，
故圆心C₂在直线x+y=4上，
故a_n+a_2015-n=4，
故数列{a_n}的所有项的和为
（a₁+a₂₀₁₄）+（a₂+a₂₀₁₃）+…（a₁₀₀₇+a₁₀₀₈）=4×1007=4028，
故选：A．

点评 本题考查了圆与圆的位置关系的判断及并项求和法的应用．