题目内容
已知函数f(x)=3x,f(a+2)=18,g(x)=λ•3ax-4x定义域[0,1].
(1)求a的值;
(2)若函数g(x)在[0,1]上是单调递减函数,求实数λ的取值范围;
(3)若函数g(x)的最大值为
,求实数λ的值.
(1)求a的值;
(2)若函数g(x)在[0,1]上是单调递减函数,求实数λ的取值范围;
(3)若函数g(x)的最大值为
| 1 |
| 2 |
考点:指数函数综合题
专题:函数的性质及应用
分析:(1)由条件f(a+2)=18建立关于a的等量关系,求出a即可;
(2)将(1)的a代入得g(x)=λ•2x-4x,g(x)在区间[0,1]上是单调递减函数,可利用函数单调性的定义建立恒等关系,分离出λ,求出2x2+2x1的最值即可.
(3)设2x=t,原题转化为y=-t2+λt=-(t-
)2+
,t∈[1.2]最大值为
,求实数λ的值.对λ分类讨论,求出在区间[1,2]上的最大值,使其等于
,解出λ即可.
(2)将(1)的a代入得g(x)=λ•2x-4x,g(x)在区间[0,1]上是单调递减函数,可利用函数单调性的定义建立恒等关系,分离出λ,求出2x2+2x1的最值即可.
(3)设2x=t,原题转化为y=-t2+λt=-(t-
| λ |
| 2 |
| λ2 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵函数f(x)=3x,f(a+2)=18,
∴3a+2=18,
∴3a=2,
∴a=log32
(2)此时g(x)=λ•2x-4x
设0≤x1<x2≤1,因为g(x)在区间[0,1]上是单调减函数,
所以g(x1)-g(x2)=(2x2-2x1)(-λ+2x2+2x1)≥0成立,
∵2x2-2x1>0,
∴λ≤2x2+2x1恒成立由于2x2+2x1≥20+20=2,
所以实数λ的取值范围是λ≤2.
(3)∵函数f(x)=λ•2x-4x的定义域为[0,1],最大值为
,
由(2)知,y=-t2+λt=-(t-
)2+
,t∈[1.2],
∴对称轴方程为t=
,
①当
<1时,y=-(t-
)2+
在[1.2]是减函数,
∴当t=1时,y取最大值ymax=-(1-
)2+
=
,解得λ=
.
②当1≤
≤2时,当t=
时,y取最大值ymax=-(
-
)2+
=
,解得λ=±
,(舍)
③当
>2时,当t=2时,y取最大值ymax=-(2-
)2+
=
,解得λ=
(舍)
综上所述,实数λ的值为
.
∴3a+2=18,
∴3a=2,
∴a=log32
(2)此时g(x)=λ•2x-4x
设0≤x1<x2≤1,因为g(x)在区间[0,1]上是单调减函数,
所以g(x1)-g(x2)=(2x2-2x1)(-λ+2x2+2x1)≥0成立,
∵2x2-2x1>0,
∴λ≤2x2+2x1恒成立由于2x2+2x1≥20+20=2,
所以实数λ的取值范围是λ≤2.
(3)∵函数f(x)=λ•2x-4x的定义域为[0,1],最大值为
| 1 |
| 2 |
由(2)知,y=-t2+λt=-(t-
| λ |
| 2 |
| λ2 |
| 4 |
∴对称轴方程为t=
| λ |
| 2 |
①当
| λ |
| 2 |
| λ |
| 2 |
| λ2 |
| 4 |
∴当t=1时,y取最大值ymax=-(1-
| λ |
| 2 |
| λ2 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
②当1≤
| λ |
| 2 |
| λ |
| 2 |
| λ |
| 2 |
| λ |
| 2 |
| λ2 |
| 4 |
| 1 |
| 2 |
| ||
| 2 |
③当
| λ |
| 2 |
| λ |
| 2 |
| λ2 |
| 4 |
| 1 |
| 2 |
| 9 |
| 4 |
综上所述,实数λ的值为
| 3 |
| 2 |
点评:本题考查了利用导数研究函数的单调性,以及函数恒成立问题,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知θ为第二象限角,sinθ,cosθ是关于x的方程2x2+(
-1)x+m=0(m∈R)的两根,则sinθ-cosθ的等于( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
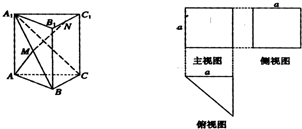 一个多面体的三视图及直观图如图所示,M、N分别是A1B、B1C1的中点.
一个多面体的三视图及直观图如图所示,M、N分别是A1B、B1C1的中点.