Question

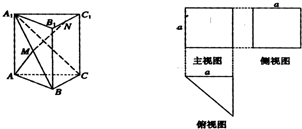一个多面体的三视图及直观图如图所示，M、N分别是A₁B、B₁C₁的中点．
（1）求证：MN⊥平面A₁BC；
（2）求异面直线AM和CA₁所成的角；
（3）求二面角A-A₁B-C的大小．

Answer 1

考点：二面角的平面角及求法,异面直线及其所成的角

专题：空间角

分析：（1）根据线面垂直的判定定理即可证明MN⊥平面A₁BC；
（2）根据异面直线所成角的定义即可求异面直线AM和CA₁所成的角；
（3）利用向量法即可求二面角A-A₁B-C的大小．

解答： 解：由三视图可知，在这个多面体的直观图中，AA₁⊥平面ABC．
且AC⊥BC，AC=BC=CC₁=a…（1分）
（1）连结AC₁，AB1，因为BC⊥平面ACC₁A₁，所以BC⊥AC₁…（2分）
在正方形ACC₁A₁中，A₁C⊥AC₁
又因为BC∩A₁C=C，所以AC₁⊥平面A₁BC…（3分）
由矩形性质得，AB₁过A₁B的中点M，
在△AB₁C₁中，由中位线性质得MN∥AC₁，
得MN⊥平面A₁BC…（4分）
（2）由题意CB，CA，CC₁两两垂直，故以C为原点，CB，CA，
CC₁所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，
又AC=BC=CC₁=a，则B（a，0，0）B₁（a，0，a），A（0，a，0），
C（0，0，0），C₁（0，0，a），…（5分）
A₁（0，a，a），则M(

a

2

，

a

2

，

a

2

)∴

AM

=(

a

2

，-

a

2

，

a

2

)，

CA1

=(0，a，a)∴

AM

•

CA1

=0…（7分）
∴异面直线AM和CA₁所成的角为90°…（8分）
（3）AB中点E的坐标为（

a

2

，

a

2

，0)

AC1

=(0，-a，a)，易知

CE

=(

a

2

，

a

2

，0)为平面AA₁B的法向量．
又AC₁⊥平面A₁BC，故

AC1

为平面A₁BC的法向量…（10分）
设二面角A-A₁B-C为θ，则
|cosθ|=|cos＜

CE

，

A1C

＞|=|

CE • AC1

| CE || AC1 |

|=|

- a2 2

2 2 a× 2 a

|=

1

2

…（12分）
由题意可知，θ为锐角，所以θ=60°，即二面角为A---A₁B---C为60°…（13分）

点评：本题主要考查空间角的求解，要求熟练掌握异面直线所成的角以及空间二面角的求解．