题目内容
 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.(1)求证:AC1∥平面CDB1;
(2)求异面直线AC与BC1所成角的大小.
考点:直线与平面平行的判定,异面直线及其所成的角
专题:空间位置关系与距离
分析:(I)设BC1与CB1交于点O,连接OD,利用三角形中位线性质,证明OD∥AC1,利用线面平行的判定,可得AC1∥平面CDB1.
(Ⅱ)因为AC∥A1C1,得到异面直线AC与BC1所成角为∠BC1A1,通过勾股定理的逆定理可求为90°.
(Ⅱ)因为AC∥A1C1,得到异面直线AC与BC1所成角为∠BC1A1,通过勾股定理的逆定理可求为90°.
解答:
(I)证明:设BC1与CB1交于点O,则O为BC1的中点.
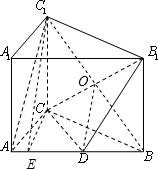
在△ABC1中,连接OD,∵D,O分别为AB,BC1的中点,
∴OD为△ABC1的中位线,
∴OD∥AC1,
又AC1?平面CDB1,OD?平面CDB1,
∴AC1∥平面CDB1.
(Ⅱ)解:∵AC∥A1C1,
∴异面直线AC与BC1所成的角为∠BC1A1,
∵在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,
∴A1B2=AA12+AB2=41,BC12=CC12+BC2=32,A1C12=9,
∴A1B2=BC12+A1C12,
∴∠A1C1B=90°,
∴异面直线AC与BC1所成角的大小为90°.

在△ABC1中,连接OD,∵D,O分别为AB,BC1的中点,
∴OD为△ABC1的中位线,
∴OD∥AC1,
又AC1?平面CDB1,OD?平面CDB1,
∴AC1∥平面CDB1.
(Ⅱ)解:∵AC∥A1C1,
∴异面直线AC与BC1所成的角为∠BC1A1,
∵在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,
∴A1B2=AA12+AB2=41,BC12=CC12+BC2=32,A1C12=9,
∴A1B2=BC12+A1C12,
∴∠A1C1B=90°,
∴异面直线AC与BC1所成角的大小为90°.
点评:本题考查了直三棱柱中的线面关系以及线线关系,熟练直棱柱的性质是解答的关键.

练习册系列答案
相关题目
已知定义在R上的函数f(x)满足xf′(x)+f(x)>0,当0<a<b<1时,下面选项中最大的一项是( )
| A、abf(ab) |
| B、baf(ba) |
| C、logab•f(logab) |
| D、logba•f(logba) |