题目内容
1.若f(x)是定义在R上的可导函数,且对任意x∈R,满足f(x)+f'(x)>0,则对任意实数a,b( )| A. | a>b?eaf(b)>ebf(a) | B. | a>b?eaf(b)<ebf(a) | C. | a>b?eaf(a)<ebf(b) | D. | a>b?eaf(a)>ebf(b) |
分析 根据条件构造函数令g(x)=exf(x),由求导公式和法则求出g′(x),根据条件判断出g′(x)的符号,得到函数g(x)的单调性,利用g(x)的单调性可求出.
解答 解:由题意令g(x)=exf(x),
则g′(x)=ex[f(x)+f'(x)]
∵f(x)+f'(x)>0,
∴g′(x)>0,
即g(x)在R上是单调递增,
①若a>b,
∴g(a)>g(b),
∴eaf(a)>ebf(b),
②若eaf(a)>ebf(b),
∴g(a)>g(b),
∴a>b
∴a>b?eaf(a)>ebf(b)
故选:D
点评 本题主要考查导数与函数的单调性关系,以及利用条件构造函数,考查学生的解题构造能力和转化思想.

练习册系列答案
相关题目
9.执行如图所示的程序框图,若输出的结果为S=1320,则判断框内应填入的内容是( )


| A. | K<9? | B. | K<10? | C. | K<11? | D. | K<12? |
6.已知过曲线$\left\{\begin{array}{l}{x=3sinθ}\\{y=3cosθ}\end{array}\right.$(θ为参数,0≤θ≤π)上一点P与原点O的直线PO的倾斜角为$\frac{π}{2}$,则P点坐标是( )
| A. | (0,3) | B. | $(-\frac{12}{5},-\frac{12}{5})$ | C. | (-3,0) | D. | $(\frac{12}{5},\frac{12}{5})$ |
13.执行如图所示的程序框图,则输出s的值等于( )
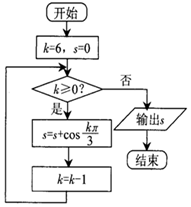

| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 1 |
10.如图是“二分法”求方程近似解的流程图,在①,②处应填写的内容分别是( )
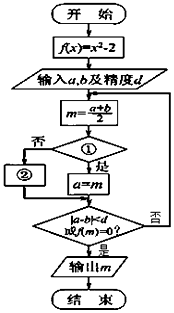

| A. | f(a)•f(m)<0?;b=m | B. | f(b)•f(m)<0?;b=m | C. | f(a)•f(m)<0?;m=b | D. | f(b)•f(m)<0?;b=m |
11.设集合A={-1,0,1,2,3},B={x|x2-2x>0},则A∩(∁RB)=( )
| A. | {-1,3} | B. | {0,1,2} | C. | {1,2,3} | D. | {0,1,2,3} |