题目内容
2.我国古代数学名著《九章算术》的论割圆术中有:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”它体现了一种无限与有限的转化过程.比如在表达式1+$\frac{1}{1+\frac{1}{1+…}}$中“…”即代表无数次重复,但原式却是个定值,它可以通过方程1+$\frac{1}{x}$=x求得x=$\frac{\sqrt{5}+1}{2}$.类比上述过程,则$\sqrt{3+2\sqrt{3+2\sqrt{…}}}$=( )| A. | 3 | B. | $\frac{\sqrt{13}+1}{2}$ | C. | 6 | D. | 2$\sqrt{2}$ |
分析 通过已知得到求值方法:先换元,再列方程,解方程,求解(舍去负根),再运用该方法,注意两边平方,得到方程,解出方程舍去负的即可.
解答 解:由已知代数式的求值方法:
先换元,再列方程,解方程,求解(舍去负根),
可得要求的式子.
令$\sqrt{3+2\sqrt{3+2\sqrt{…}}}$=m(m>0),
则两边平方得,则3+2$\sqrt{3+2\sqrt{3+2\sqrt{…}}}$=m2,
即3+2m=m2,解得,m=3,m=-1舍去.
故选:A
点评 本题考查类比推理的思想方法,考查从方法上类比,是一道基础题.

练习册系列答案
相关题目
13.执行如图所示的程序框图,则输出s的值等于( )
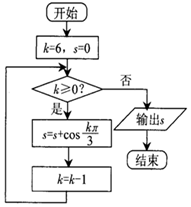

| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 1 |
10.如图是“二分法”求方程近似解的流程图,在①,②处应填写的内容分别是( )
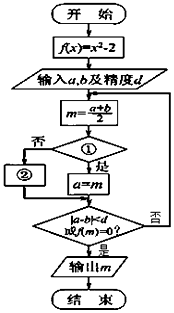

| A. | f(a)•f(m)<0?;b=m | B. | f(b)•f(m)<0?;b=m | C. | f(a)•f(m)<0?;m=b | D. | f(b)•f(m)<0?;b=m |
14.《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输入的S,T的值分别为40,126,则输出a,b的值分别为( )
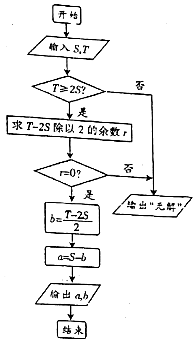

| A. | 17,23 | B. | 21,21 | C. | 19,23 | D. | 20,20 |
11.设集合A={-1,0,1,2,3},B={x|x2-2x>0},则A∩(∁RB)=( )
| A. | {-1,3} | B. | {0,1,2} | C. | {1,2,3} | D. | {0,1,2,3} |
12.执行如图的程序框图,如果输入的x1=2000,x2=2,x3=5,则输出的b的值为( )


| A. | 1 | B. | 2 | C. | 4 | D. | 5 |
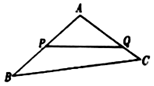 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.