题目内容
4.把参数方程$\left\{\begin{array}{l}{x=\frac{4k}{1-{k}^{2}}}\\{y=\frac{4{k}^{2}}{1-{k}^{2}}}\end{array}\right.$(k为参数)化为普通方程,并说明它表示什么曲线.分析 由已知得y=$\frac{4{k}^{2}}{1-{k}^{2}}$=k×$\frac{4k}{1-{k}^{2}}$=kx,从而k=$\frac{y}{x}$,由此能求出该参数方程的普通方程.
解答 解:∵参数方程$\left\{\begin{array}{l}{x=\frac{4k}{1-{k}^{2}}}\\{y=\frac{4{k}^{2}}{1-{k}^{2}}}\end{array}\right.$(k为参数),
∴y=$\frac{4{k}^{2}}{1-{k}^{2}}$=k×$\frac{4k}{1-{k}^{2}}$=kx,
∴该参数方程的普通方程为y=kx,∴k=$\frac{y}{x}$,
∴x=$\frac{4×\frac{y}{x}}{1-\frac{{y}^{2}}{{x}^{2}}}$,整理,得该曲线的普通方程为x2-y2-4y=0.
它表示焦点在y轴上的双曲线.
点评 本题考查曲线的普通方程的求法,考查直角坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
9.执行如图所示的程序框图,若输出的结果为S=1320,则判断框内应填入的内容是( )


| A. | K<9? | B. | K<10? | C. | K<11? | D. | K<12? |
13.执行如图所示的程序框图,则输出s的值等于( )
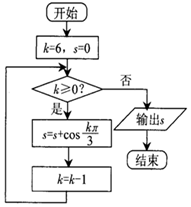

| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 1 |
14.《孙子算经》是我国古代内容极为丰富的数学名著,其中一个问题的解答可以用如图的算法来实现,若输入的S,T的值分别为40,126,则输出a,b的值分别为( )
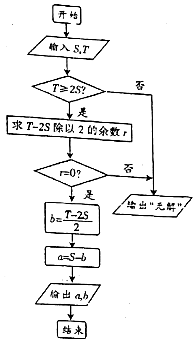

| A. | 17,23 | B. | 21,21 | C. | 19,23 | D. | 20,20 |