题目内容
已知点A,B的坐标分别为(-2,0),(2,0).直线AP,BP相交于点P,且它们的斜率之积是-
,记动点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)设Q是曲线C上的动点,直线AQ,BQ分别交直线l:x=4于点M,N,线段MN的中点为D,求直线QB与直线BD的斜率之积的取值范围;
(3)在(2)的条件下,记直线BM与AN的交点为T,试探究点T与曲线C的位置关系,并说明理由.
| 1 |
| 4 |
(1)求曲线C的方程;
(2)设Q是曲线C上的动点,直线AQ,BQ分别交直线l:x=4于点M,N,线段MN的中点为D,求直线QB与直线BD的斜率之积的取值范围;
(3)在(2)的条件下,记直线BM与AN的交点为T,试探究点T与曲线C的位置关系,并说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设出点P的坐标,表示出直线AM、BM的斜率,求出它们的斜率之积,利用斜率之积是-
,建立方程,去掉不满足条件的点,即可得到点M的轨迹方程;
(2)直线AQ的方程为y=k(x+2),令x=4,则得M的坐标,直线BQ的方程为y=-
(x-2),令x=4,则得N的坐标,可得D的坐标,求直线QB与直线BD的斜率之积,即可求出其取值范围;
(3)由(2)得,M(4,6k),N(4,-
),利用直线BM与AN的斜率之积是-
,可得结论.
| 1 |
| 4 |
(2)直线AQ的方程为y=k(x+2),令x=4,则得M的坐标,直线BQ的方程为y=-
| 1 |
| 4k |
(3)由(2)得,M(4,6k),N(4,-
| 1 |
| 2k |
| 1 |
| 4 |
解答:
解:(1)设P(x,y),因为A(-2,0),B(2,0)
∴由已知,
•
=-
(x≠±2)
化简,得
+y2=1(x≠±2).…(4分)
(2)设直线AQ的斜率为k(k≠0),则由题可得直线BQ的斜率为-
,
∴直线AQ的方程为y=k(x+2),令x=4,则得M(4,6k),
直线BQ的方程为y=-
(x-2),令x=4,则得N(4,-
),
∴D(4,3k-
),
∴kBD=
=
-
…(8分)
故kBDkQB=(
-
)×(-
)=-
+
>-
,
∴直线QB与直线BD的斜率之积的取值范围为(-
,+∞)…(10分)
(3)由(2)得,M(4,6k),N(4,-
),
∴kBM•kAN=
•
=-
…(12分)
∴点T在曲线C上.…(14分)
∴由已知,
| y |
| x+2 |
| y |
| x-2 |
| 1 |
| 4 |
化简,得
| x2 |
| 4 |
(2)设直线AQ的斜率为k(k≠0),则由题可得直线BQ的斜率为-
| 1 |
| 4k |
∴直线AQ的方程为y=k(x+2),令x=4,则得M(4,6k),
直线BQ的方程为y=-
| 1 |
| 4k |
| 1 |
| 2k |
∴D(4,3k-
| 1 |
| 4k |
∴kBD=
3k-
| ||
| 4-2 |
| 3k |
| 2 |
| 1 |
| 8k |
故kBDkQB=(
| 3k |
| 2 |
| 1 |
| 8k |
| 1 |
| 4k |
| 3 |
| 8 |
| 1 |
| 32k2 |
| 3 |
| 8 |
∴直线QB与直线BD的斜率之积的取值范围为(-
| 3 |
| 8 |
(3)由(2)得,M(4,6k),N(4,-
| 1 |
| 2k |
∴kBM•kAN=
| 6k-0 |
| 4-2 |
-
| ||
| 4+2 |
| 1 |
| 4 |
∴点T在曲线C上.…(14分)
点评:本题重点考查轨迹方程的求解,解题的关键是正确表示出直线AM、BM的斜率,利用条件建立方程.

练习册系列答案
相关题目

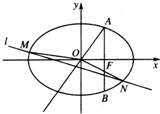 如图,已知椭圆C:
如图,已知椭圆C: