题目内容
 如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且PA=AE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
考点:直线与平面所成的角
专题:计算题,证明题,空间位置关系与距离,空间角
分析:(1)运用线面平行的判定定理和性质定理即可证得;
(2)由于PA⊥底面ABCDE,底面AMDE为正方形,建立如图的空间直角坐标系Axyz,分别求出A,B,C,E,P,F,及向量BC的坐标,设平面ABF的法向量为n=(x,y,z),求出一个值,设直线BC与平面ABF所成的角为α,运用sinα=|cos<n,
>|,求出角α;设H(u,v,w),再设
=λ
(0<λ<1),用λ表示H的坐标,再由n•
=0,求出λ和H的坐标,再运用空间两点的距离公式求出PH的长.
(2)由于PA⊥底面ABCDE,底面AMDE为正方形,建立如图的空间直角坐标系Axyz,分别求出A,B,C,E,P,F,及向量BC的坐标,设平面ABF的法向量为n=(x,y,z),求出一个值,设直线BC与平面ABF所成的角为α,运用sinα=|cos<n,
| BC |
| PH |
| PC |
| AH |
解答:
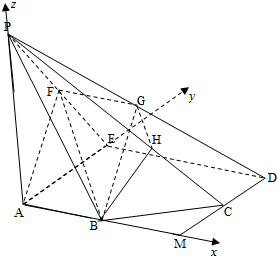 (1)证明:在正方形AMDE中,∵B是AM的中点,
(1)证明:在正方形AMDE中,∵B是AM的中点,
∴AB∥DE,又∵AB?平面PDE,∴AB∥平面PDE,
∵AB?平面ABF,且平面ABF∩平面PDE=FG,
∴AB∥FG;
(2)解:∵PA⊥底面ABCDE,∴PA⊥AB,PA⊥AE,
如图建立空间直角坐标系Axyz,则A(0,0,0),
B(1,0,0),C(2,1,0),P(0,0,2),
E(0,2,0),F(0,1,1),
=(1,1,0),
设平面ABF的法向量为n=(x,y,z),则
即
,
令z=1,则y=-1,∴n=(0,-1,1),
设直线BC与平面ABF所成的角为α,则
sinα=|cos<n,
>|=|
|=
,
∴直线BC与平面ABF所成的角为
,
设H(u,v,w),∵H在棱PC上,∴可设
=λ
(0<λ<1),
即(u,v,w-2)=λ(2,1,-2),∴u=2λ,v=λ,w=2-2λ,∵n是平面ABF的法向量,
∴n•
=0,即(0,-1,1)•(2λ,λ,2-2λ)=0,解得λ=
,∴H(
,
,
),
∴PH=
=2.
 (1)证明:在正方形AMDE中,∵B是AM的中点,
(1)证明:在正方形AMDE中,∵B是AM的中点,∴AB∥DE,又∵AB?平面PDE,∴AB∥平面PDE,
∵AB?平面ABF,且平面ABF∩平面PDE=FG,
∴AB∥FG;
(2)解:∵PA⊥底面ABCDE,∴PA⊥AB,PA⊥AE,
如图建立空间直角坐标系Axyz,则A(0,0,0),
B(1,0,0),C(2,1,0),P(0,0,2),
E(0,2,0),F(0,1,1),
| BC |
设平面ABF的法向量为n=(x,y,z),则
|
|
令z=1,则y=-1,∴n=(0,-1,1),
设直线BC与平面ABF所成的角为α,则
sinα=|cos<n,
| BC |
n•
| ||
|n|•|
|
| 1 |
| 2 |
∴直线BC与平面ABF所成的角为
| π |
| 6 |
设H(u,v,w),∵H在棱PC上,∴可设
| PH |
| PC |
即(u,v,w-2)=λ(2,1,-2),∴u=2λ,v=λ,w=2-2λ,∵n是平面ABF的法向量,
∴n•
| AH |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
∴PH=
(
|
点评:本题主要考查空间直线与平面的位置关系,考查直线与平面平行、垂直的判定和性质,同时考查直线与平面所成的角的求法,考查运用空间直角坐标系求角和距离,是一道综合题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 如图,O为坐标原点,双曲线C1:
如图,O为坐标原点,双曲线C1: